C, PHP, VB, .NET

Нека е даден квадрат, чиято страна е с дължина [mathi]l[/mathi]. Върху страните на квадрата са избрани произволни точки [mathi]P[/mathi] и [mathi]Q[/mathi]. Каква е вероятността [mathi]|PQ|>l?[/mathi]?

Решение: Нека означим върховете на квадрата [mathi]ABCD[/mathi] така, че т.[mathi]P[/mathi] да лежи на [mathi]AB[/mathi]. Пример за един от възможните случаи е показан на следната картинка:

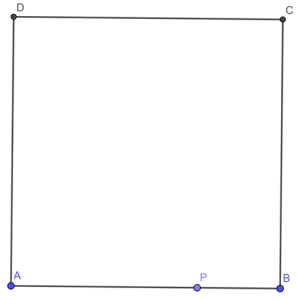
Имаме четири възможни случая за т.[mathi]Q[/mathi], които са с равна вероятност.

1 случай) Ако т.[mathi]Q[/mathi] лежи на [mathi]AB[/mathi], тогава [mathi]P(|PQ|>l) = 0[/mathi]

2 случай) Ако т.[mathi]Q[/mathi] лежи на [mathi]CD[/mathi], тогава [mathi]P(|PQ|>l) = 1[/mathi]

3 случай) Ако т.[mathi]Q[/mathi] лежи на [mathi]AD[/mathi], ще разгледаме центъра на отсечката [mathi]PQ[/mathi]. Построяваме кръг с център т.[mathi]A[/mathi] и радиус [mathi]\frac{l}{2}[/mathi]. Експериментално може да се провери, че ако [mathi]PQ > l[/mathi], то центъра на [mathi]PQ[/mathi], който ще означим с т.[mathi]M[/mathi] ще лежи вътре в сектора, който се образува при пресичането на кръга с квадрата:

 

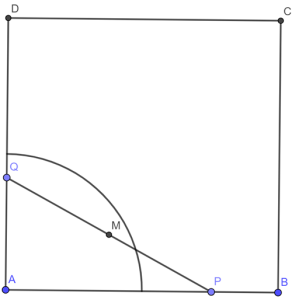
Това е така, защото ако означим [mathi]|AP| = x[/mathi] и [mathi]|AQ| = y[/mathi], то

[math]|AM|=|PM|=\frac{|PQ|}{2}=\sqrt{\frac{x^2}{4}+\frac{y^2}{4}}[/math]

Когато т.[mathi]M[/mathi] е вътре в сектора, [mathi]\sqrt{\frac{x^2}{4}+\frac{y^2}{4}} < \frac{l}{2}[/mathi], откъдето [mathi]\frac{|PQ|}{2}<\frac{l}{2}[/mathi] или [mathi]PQ<l[/mathi].

Следователно отсечката ще бъде по-дълга от [mathi]l[/mathi] тогава, когато т.[mathi]M[/mathi] е извън него. Това е лицето на защрихованата част от следната картинка.

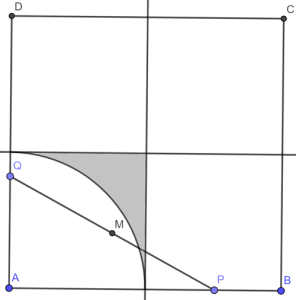
Вероятността т.[mathi]M[/mathi] да е вътре в тази зона е:

[math]P(M\notin сектора)=1-P(M\in сектора) = 1-\frac{S(сектора)}{S(малкия квадрат)}=1-\frac{\frac{1}{4}\pi (\frac{l}{2})^2}{(\frac{l}{2})^2}=1-\frac{\pi}{4}[/math]

4 случай) Ако т.[mathi]Q[/mathi] лежи на [mathi]BC[/mathi], вероятността ще е същата както в случай 3, защото решенията са симетрични.

От тук решението на задачата е обединението на тези четири случая, т.е.:

[math]P(|PQ|>l) = \frac{0+1+1-\frac{\pi}{4}+1-\frac{\pi}{4}}{4}=\frac{6-\pi}{8}[/math]