C, PHP, VB, .NET

Теория на вероятностите е една позната за математиците дисциплина. Рядко обаче те се сблъскват с т.нар. "геометрични вероятности". Това са задачи, които използват апарата на теория на вероятностите върху задачи от геометрията. Например:

Задача: Нека AB е отсечка и т.M∈AB. Нека отсечката PQ∈AB. Каква е вероятността т.M∈PQ да е вярно?

Решение: Нека |AB|=l. Нека вероятността M∈PQ = P(PQ). Тази вероятност е пропорционална на дължината на PQ (колкото по-дълга е отсечка PQ толкова по-голяма е вероятността P(PQ)), т.е. P(PQ)=λ|PQ| (1).

Понеже по  условие т.M∈AB, то вероятността P(AB)=1
=> 1=λ|AB| => λ = 1 / |AB|
=> Заместваме λ в (1):

Това е основната задача в геометричните вероятности. За по-опростен запис ще приемем, че ако |PQ|=h и |AB|=l, то P(PQ)=P(h)=h/l. Валидни са следните закони:

Закон за събиране: P(x+y) = P(x) + P(y)

Закон за скалиране: P(nx) = n.P(x), където nx ≤ l.

Вероятността при отсечки беше разгледана в едномерното пространство. Лесно можем да пренесем по аналогия същата формула в двумерното пространство. Нека A е област в равнината с лице S и нека a∈A е нейна подобласт с лице δ. Тогава вероятността на т.M∈A да попадне в областта a е:

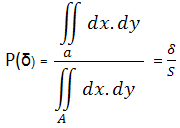Аналогично можем да изведем геометрична вероятност в пространството - ако V' е област в пространството с обем V, а v'∈V' е нейна подобласт с обем v, то вероятността на една точка M∈V' да попадне и във v' е:

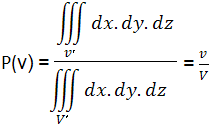
По същия начин можем да изведем други елементарни геометрични вероятности. Нека например имаме точка О в равнината. Нека имаме лъч l започващ от точка O. Нека имаме сегмент от окръжност с център точката O. Ако сегментът е цялата окръжност (тоест ъгъл 2π), то лъча със сигурност ще премине през сегмента. Ако сегментът обаче е по-малък (с ъгъл ρ), то вероятността P(ρ) = ρ/2π.

Накрая - ако имаме функция f(x)  в едномерното пространство върху област (o, l), то нейната средна стойност е:

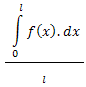
Средна стойност на функция f(x,y) в двумерното пространство ще бъде:

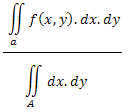
Аналогично се дефинира и средна стойност на функция за тримерното пространство...