* Положение на две точки в кръг
Публикувано на 07 февруари 2010 в раздел Вероятности.
Задача: Нека имаме кръг k с радиус R и две точки M1∈k и M2∈k. Каква е вероятността дължината на отсечката |M1M2|≤h<2R?
Решение: Построяваме координатна система с център центъра на кръга. Нека точките M1 и M2 имат следните координати спрямо нея: M1(x1,y1) и M2(x2,y2). Тогава условията които трябва да удовлетворяват M1 и M2 са:
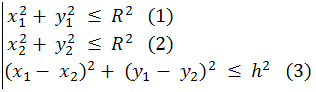Елементарните вероятности са:
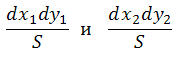където S = π.R2 => вероятността P(|M1M2|≤h) е:
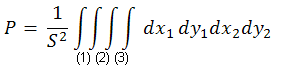
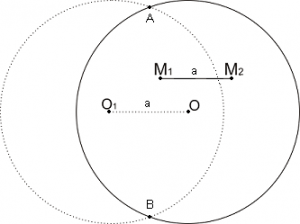
Сега ще трябва да решим този интеграл. Нека дължината |M1M2| = a. Построяваме нова окръжност k1 с център O1, като:
1) |OO1| = a;
2) OO1 || M1M2.
Нека ъгъла между абцисата на координатната система Ox и M1M2 е <(Ox,M1M2)=θ, 0≤θ≤2π.
Ако разгледаме направлението OO1 като транслация то точка M2 се изобразява в точка M1. За да бъде M2 вътре в кръга k, то трябва M1 да принадлежи на общата част на двата кръга. Нека ъгъл <(AOB) = u, като 2.arccos(h/2R)≤u≤π.
=> |M1M2| = a = 2Rcos(u/2)
Общата част на двата кръга е с лице R2(u-sin(u)).
=> 
=> 
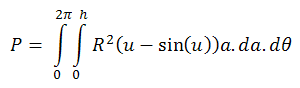
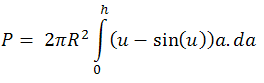
Ако h.2R = sin(α/2) (α може да се намери), то π-a<u<π. Също така a.da=-R2sin(u)du.
=> 
=> 
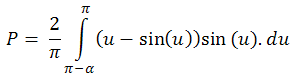
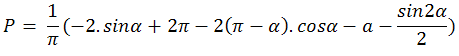
Заместваме cosα = 1-2.sin2(α/2) = (2R-h2)/2R2.
=> Окончателно: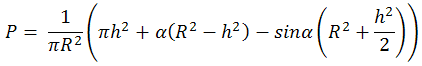
Задача: Решете аналогичната задача, но в пространството със сфера. Използвайте полярни координати за координатната система.
Добави коментар