C, PHP, VB, .NET

Задача: Имате отсечка, която "чупите" на три части. Каква е вероятността тези части да образуват триъгълник?

Решение: Както и в предишните разгледани задачи, и тук задачата има различна гъстота на решенията в зависимост от интерпретацията на началното условие. Нека разгледаме четири варианта на избор:

1) Избирате две произволни точки върху отсечката и я "чупите" по тях.

Ще използваме интерпретация на теоремата на Винченцо Вивиани, а именно:

(T) Сборът от разстоянията от вътрешна в равностранен триъгълник точка до неговите страни e един и същ за всяка вътрешна точка.

Нека отсечката е с дължина l. Тогава можем да построим равностранен триъгълник такъв, че сборът от разстоянията от която и да е вътрешна точка до страните му е равен на l. Така всяка точка, лежаща в този триъгълник, може да се разглежда като произволно разделяне на отсечката на три равни части.

Сега да разгледаме равностранния триъгълник със страни медицентровете на страните на този триъгълник:

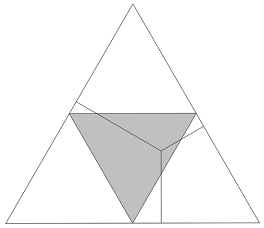
Лесно може да се прецени и докаже, че ако точката лежи вътре в малкия триъгълник, то трите отсечки (разстояния до страните на големия) ще изпълняват условието за съществуване на триъгълник, а ако точката е извън малкия триъгълник, то условието за съществуване на триъгълник няма да бъде изпълнено. Така трите части на отсечката да образуват триъгълник се оказва 1/4.

2) Избирате произволна точка и "чупите" отсечката веднъж. Тогава избирате по-дългото от двете парчета и също го "чупите" на две парчета.

Тук тренираният читател сам ще забележи, че има отклонение в условието. Първата точка на "чупене" е избрана произволно от отсечка с дължина "l". За удобство ще приемем, ме l=1. Нека тя е "разчупила" къса отсечка "x" и дълга "1-x". Второто чупене също е произволно, но забележете - вече не върху отсечка с дължина 1, а върху отсечка с дължина 1-x. Ако разгледаме по аналогия с предишната задача, то вече сме определили едната височина (x):

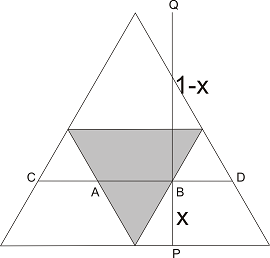
Така точката ще се движи по отсечката CD. Ако тя попадне в AB, то ще имаме триъгълник. Ако не - няма да имаме. Да, но AB и CD зависят от x, и по-точно AB/CD = x/(1-x). Така, понеже знаем, че x<1/2, можем да изчислим вероятността като:

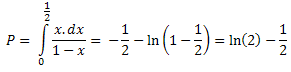
Виждаме, че вероятността както очаквахме е различна - приблизително 0,193. Да, но това беше при положение, че сме "счупили" парчето x<1/2 (това беше наше предположение, с което всъщност ограничаваме решението). Какво ще се случи ако парчето x>1/2? Ще имаме абсолютно "огледална" задача, където интеграла ще бъде в граници от 1/2 до 1. Тоест общото решение ще е "двойно" по-голямо от решението от интеграла по-горе или приблизително 0,386 или грубо 2/5.

3) Избирате произволна точка и "чупите" отсечката веднъж. Тогава избирате произволно едно от парчетата и го "чупите", като по този начин получавате трите отсечки.

Тук много хора интуитивно се насочват, че вероятността е същата както в първата точка. Истината е съвсем друга. Тук имаме два случая:

1: Избрали сме по-малката отсечка, т.е. едната от отсечките ще е винаги по-голяма от половината от дължината на цялата отсечка, т.е. вероятността да формираме триъгълник тук е 0;

2: Избрали сме по-голямата отсечка, т.е. от тук нататък вероятността да формираме триъгълник ще е както в предишната задача от точка 2).

Вероятността да попаднем в едната от двете изброени възможности е 1/2. Така общо получаваме, че вероятността е наполовина на вероятността от точка 2), т.е. около 0,193 или грубо 1/5.

4) Избирате произволна точка и "чупите" отсечката веднъж. Тогава избирате произволно едно от парчетата, но пропорционално на дължината им, и го "чупите".

Тук имаме същата задача както 3), но с тази разлика, че не взимаме отсечките с вероятност 1/2, а ги взимаме с вероятност зависима от първото счупване. Нека за удобство отново дължината на отсечката е l=1. Тогава ако първото счупване е разделило отсечката на x и 1-x отсечки (x<1/2), то вероятността да изберем по-малката е x, а вероятността да изберем по-голямата е 1-x. От тук, както и в предишния случай, имаме два варианта:

1: Избрали сме по-малката отсечка

=> независимо как я счупим няма да получим триъгълник

2: Избрали сме по-голямата отсечка, т.е. 1-x. Тук е уместно да погледнем отново графиката от вариант на решение 2):

За да бъде формиран триъгълник отново имаме вероятността AB/CD = x/(1-x), но този път с добавено условие вероятността (1-x) (от избора), т.е. общо: (1-x).x/(1-x) = x. Интегрираме по границите на x:

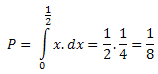
Тук обаче отново, както в задача 2 отбелязваме, че ограничихме x<1/2, т.е. отново имаме "огледално" решение при x>1/2, т.е. се налага накрая да "удвояваме резултата" от интеграла. Така се получава, че общата вероятност в този случай е 1/4.

Отговорите с случай 1) и случай 4) съвпаднаха. С малко повече анализ можете да докажете, че техните условия са напълно еквивалентни!

Използвана литература:

1. Мартин Гарднър - "Математически Развлечения", том 2.