* Апория в двумерното пространство
Публикувано на 04 ноември 2010 в раздел Математика.
Представете си, че се намирате в квартал, чиито улици са на "каре" (на картинката по-долу това са пунктираните линии). Целта ви е да стигнете от т. А до т.B:
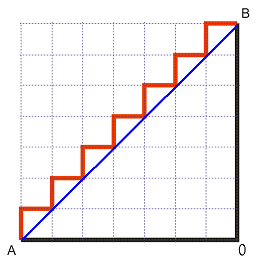
Нека приемем, че страната AO = BO = 1. Най-краткия път от A до B е по правата синя линия - sqrt(2). Ние обаче можем да се движим само по улиците.
Ако минем по дебелата черна линия (първо от A до O и после от O до B) изминатия път ще бъде 1+1 = 2. Нека обаче да се стремим да се движим максимално близко до синята линия - например по червената начупена линия. За наше нещастие ще се окаже, че отново изминатия път е 2 и нищо не сме спестили. Доказателството е елементарно.
Нека сега да кажем, че сме намерили преки пътечки в междублоковите пространства. За съжаление те са отново под прав ъгъл. Получила се е нова начупена червена линия:
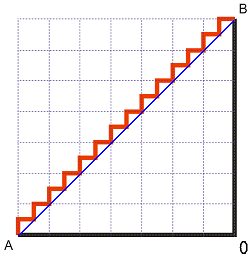
Отново лесно се пресмята, че изминатия път не се е променил - той отново е 2! Нека продължим това деление още:
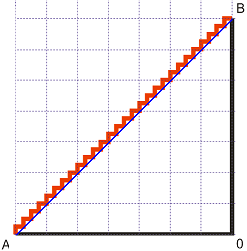
И тук изминатия път ще бъде 2!
Какво ще стане ако продължим да "наситняваме" делението още повече? Определено начупената линия все повече ще се доближава до правата синя. Изминатото разстояние по червената линия обаче ще си остава 2...
Сега обаче ще се случи нещо странно - нека продължим процеса до безкрайност. При безкрайно наситняване несъмнено червената и синята линии ще се "слеят". Значи при "наситняване" на червената линия до безкрайност ще се получи така, че изминатото разстояние по нея ще съвпадне с изминатото разстояние по синята линия, т.е. sqrt(2)!!! При всяка една реална проверка с реално число обаче разстоянието винаги ще е 2!
Този парадокс според мен е чудесен пример за апория в двумерното пространство. Правейки аналогия с апориите на Зенон се виждат много сходства - проблемът се получава именно от приравняване на дискретно начупената червена линия към непрекъснатата синя. По същия начин Зенон приравняваше дискретно времево към непрекъснато пространствено и непрекъснато времево към дискретно пространствено измерение и от там се получаваше парадокс. Лично аз правя смел индуктивен извод, че във всички пространства от всички размерности трябва да говорим за наличие на континуум. Дори бих си позволил да го напиша като работна хипотеза:
(Х) Във всяко n-мерно пространство движението е единство от непрекъснатостта и дискретността на размерностите на пространството.
Задачата е взета от блога SquareCirclez.
Добави коментар