* За ново означение на функциите…
Публикувано на 24 ноември 2010 в раздел Методика.
Когато учениците се научат да чертаят "графика на функция", те обикновено описват координатните оси като "x" и "y". Първоначално им се дават задачи от типа "y = x+2" или подобни. В един момент обаче това равенство се променя и се представя като "f(x) = x+2". Това предизвиква леко объркване и първоначално неразбиране в учениците. Те правят аналогия между двете, но обикновено не разбират защо е нужна тази промяна.
На първо време искам да вметна, че при "чертаене на графика на функция", при положение, че вече сме въвели означението "f(x)", е редно вече да не използваме осите на координатната система означени като "x" и "y", а по-добре да ги записваме правилно като "x" и "f(x)". Това би допринесло до по-добро разбиране и по-правилно означение. Това помага и в бъдеще, когато учениците трябва да изчертават графики на статистически функции - там обикновено осите имат означения на предмети от реалния свят, а не са тривиалните "x" и "y".
Как да мотивираме използването на новото означение "f(x)=...", вместо "y=..."? Отговорът трябва да дойде не по догматичен, а по логичен път. Ще дам един практически пример. Взех един лист хартия формат A4 и на него нарисувах една окръжност. Сега искам вие да вземете лист хартия и да нарисувате същата окръжност. Да, но вие не виждате моя лист. Тогава каква допълнителна информация ще изискате от мен?
Знаете, че всяка окръжност се задава чрез "център и радиус". Следователно вие ще поискате три числа - двете координати и дължината на радиуса, като предварително ще трябва да се съгласим да използваме една и съща мерна система - например сантиметри. Е, нека аз ви кажа тогава "нарисувайте окръжност с център (12,10) и радиус 5". Това вече еднозначно ще определи моята окръжност и вие лесно ще я нарисувате на вашия лист. За по-стегнато изложение можем да направим следното означение "k(x, y, R)", където обикновено "k" приемаме за понятието "окръжност" (практически можем да го въведем и като "окръжност(x, y, R)"). При параметри x=12, y=10 и R=5 за по-кратко записваме "k(12,10,5)".
Виждате, че по този начин имаме ясна представа за това "какъв е обекта". Горната функция се превежда като "дадена е функция k, която изчертава окръжност с радиус R и с координати на центъра x и y". По същия начин можем да дефинираме функция "сума(x,y)", която да представя "сбора на числата x и y". В този случай можем да запишем и математическата формула за функцията, а именно: "сума(x,y) = x+y". При функции, които изискват изчисление на алгебрична стойност това е възможно.
Сега вече е лесно да обясним какво е "f(x) = x+2". Това се превежда като "функцията с име f приема един параметър x и има алгебрична стойност x+2". От тук насетне решаваме един важен проблем - дублирането на имената на функциите. Представете си например, че трябва да изчертаете едновременно графиките на функциите "y = x+2" и "y = 2x -1". Това означение води до абсурд - "y" може да приема едновременно две различни стойности за едно и също x. Логически (за да няма абсурд) това би трябвало да ни доведе до решаване на система, в която еднозначно да определим "x = 3", а от там "y = 5". Да, но нали "x" беше променлива? Изобщо тук задачата се изопачи напълно! Ако ние обаче запишем функциите като "f(x) = x+2" и "g(x) = 2x-1", то този проблем го няма. Продължава да е наличен обаче проблемът с чертаенето на графиките на функциите в една координатна система. Ако едната ос се означи с "x", то какво ще бъде означението на другата? Редно ли е да я запишем като "f(x), g(x)"? Според мен - да!
Когато говорим за означение на функции обаче понякога се сблъскваме с друг проблем - несъответствието на действието на скобите с вече известните математически операции. Например учениците са решавали множество задачи от типа:
5(2+3) = 5.2 + 5.3 = 10 + 15 = 25
или по-обобщено
a(b+c) = ab + ac
Учениците са научени да "разкриват скобите" от предишните си знания. Следователно те биха могли спокойно да направят следното с една функция:
sin(a+b) = sin(a) + sin(b)
Да, но това знаем, че е напълно неправилно, защото "sin" е име на функция, а не параметър. Какво обаче ни пречи всъщност да имаме параметър с име "sin"? Или три параметъра - s, i и n? Ако това е така, то горния запис става напълно валиден. Не се ли получава неестествено объркване?
Може от гледната точка на времето това да е банален и елементарен за осмисляне проблем, но истината е, че в учебна среда тази грешка е срещана изключително често и този и други подобни проблеми са решени само и единствено с множество упражнения и понякога дори с догматични забрани. Това естествено губи време.
Какво различава "a(b+c)" от "f(b+c)"? Трябва предварително да знаем, че едното е функция, а другото е израз. Да, но това не винаги е толкова очевидно.
Първото решение е изключително непрактично - да изписваме винаги всичко с функции. Да, но тогава например изразът "2(3x+4)" ще трябва да се запише като "умножи(2,събери(умножи(3,x),4))". Очевидно това няма да намери практическо приложение (извън някои ограничени езици за програмиране).
Друго решение е винаги да пишем знакът за умножение, т.е. вместо "a(b+c)" да пишем "a.(b+c)". Това според мен е възможно и практично, но може би не чак толкова нагледно. Според мен по-правилното е просто да заменим скобите с друг вид. Например вместо "f(x)" да записваме функцията като "f[x]". Това ще разреши напълно проблема с двойното тълкуване! По този начин когато изпишем "f[x] = 3(x+3)" няма да имаме никакво двусмислие коя операция каква е - скобите от дясно можем да ги "разкрием" спокойно, докато тези от ляво не!.
Обобщение: предложението ми е да променим означението на скобите на параметрите на функциите, както и означенията на осите на координатните системи. Така евентуалните задачи биха изглеждали по следния начин:
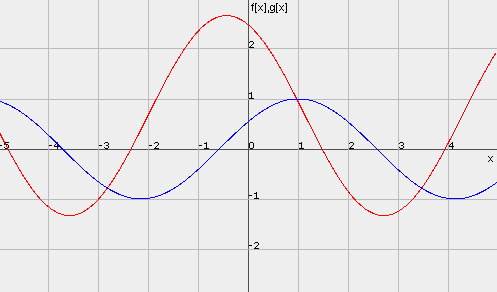
Задача: Изчертайте графиките на функциите f[x]=cos[x-1] и g[x]=2(sin[x+2]+1/3)
Решение:
Добави коментар