* Среща в автобуса
Публикувано на 12 декември 2010 в раздел Вероятности.
Задача 1: Двама приятели всеки ден пътуват с автобус до работата си. В зависимост от това кой кога е станал те обикновено пристигат на спирката на рейса произволно между 8:00 и 8:20 сутринта. И двамата са склонни да се изчакват един друг, за да пътуват заедно, но максимум до 5 минути. Каква е вероятността да пътуват заедно? Приемаме, че непрекъснато пристигат и заминават автобуси.
Решение 1: Нека изберем координатна система с оси Pt1 и Pt2, по които ще измерваме времето на пристигане на "приятел 1" и "приятел 2" в минути. За удобство началото на координатната система (0,0) приемаме, че е 8:00 часа. Така на всяка възможна комбинация от пристигане на спирката "x" за "приятел 1" и "y" на "приятел 2" съответства точка P(x,y). Всички възможни точки P определят квадрат заключен от правите Pt1=0, Pt2=0, Pt1=20 и Pt2=20:
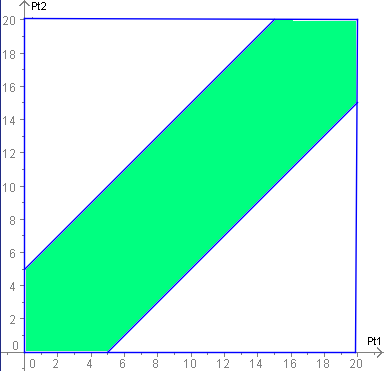
Зеленият регион на картинката е определен от линиите:
- Pt1=Pt2+5
- Pt2=Pt1-5
Виждаме, че за всяка точка P(x,y) вътре в зеления регион имаме |x - y| ≤ 5. Следователно ако точката е вътре в зеления регион, то приятелите са се срещнали, а ако не е, то не са пътували заедно. Така вероятността те да са пътували заедно е площта на зеления регион разделена на площта на квадрата.
Лицата на белите триъгълници са 15.15/2 = 112,5. Общото им лице е 225, а лицето на целия квадрат е 20.20 = 400.
Следователно вероятността да са пътували заедно е:
P = (400-225)/400 = 175/400 = 7/16 = 0,4375
Решение 2: Нека проверим решението на тази задача чрез метода от задачата за положение на две точки върху отсечка. Идеята е същата, като едната от точките ще представя пристигането на "приятел 1", а другата точка пристигането на "приятел 2". Като заместим l=20 и k=1/4, то от общото решение получаваме:
P = 2.1/4 - 1/16 = 7/16 = 0,4375
Виждаме, че методите и решенията са еквивалентни!
Задача 2. Решете същата задача, като приятелите са трима.
Задача 3. Решете същата задача при "n" на брой приятели.
Ако приятеля пристигне в 8:20, няма ли да чака до 8:25? Или той знае че щом другия го няма значи вече е минал?
Не, след 8:20 не може да се чака (ще закъснеят за работа) :)
А като са 3ма и първия ако е чакал 5 мин и е дочакал 2рия, но не е дочакал 3тия остава ли да чака още или тръгва сам, или тръгват и двамата, или остават да чакат 5те минути на втория?
Ако никой никого не чака правя една триизмерна графика подобна на първото решение. Получава се една странна фигура, която е един куб + 3 четириъгълни призми с общ обем 10 кубични минути :D, а целия куб е с обем 64 кубични минути или шанса е 10/64=0.15625.
Съвсем логичен въпрос. Всъщност задачата може да се раздели на две задачи:
1. "Човек 1" чака 5 минути. В тези 5 минути идва "човек 2". Двамата чакат нови 5 минути за "човек 3".
2. "Човек 1" чака 5 минути. В тези 5 минути идва "човек 2". Двамата заедно изчакват остатъка от 5те минути на "човек 1" за "човек 3". Този случай може да се формулира по следния начин: "каква е вероятността тримата да пристигнат на спирката в един петминутен интервал?". Предишния случай е по-сложен.
В горното ти решение нещо не ми е ясно какво правиш. Обемът на куба е 203 = 8000.
Да, понеже съкратих размерите на 5 за по-лесно смятане и после забравих да ги върна към по-големите. Това би трябвало да е решение на 2рия вариант. Нарисувах картинка на фигурата:
http://img706.imageshack.us/img706/8458/kubiprizmi.gif
За първия вариант, взимаме вероятността 1вите 2ма да се засекат т.е. 7/16 и я умножаваме по вероятността 2рите 2ма да се засекат. Става (7/16)*(7/16)=49/256.
Изглежда да е така :)
Остава задачата с "n".
Всъщност картинката нещо не ми харесва. По-скоро ми се струва, че решението трябва да е триъгълна призма с две пирамиди в двата края. Ще се опитам да я нарисувам сега...
Ако е с триъгълна призма се губи варианта например един да е дошъл в 8:00, другите двама в 8:05. Моята фигура може да се обясни също по следния начин:
Взимаме кубчето със страна 5мин в началото на к. с-ма един от най-дългите му диагонали е от (0,0,0) до (5,5,5). То обхваща всички варианти 3мата да дойдат в 1вите 5мин. Това кубче го транслираме до кубче с диагонал от (15,15,15) до (20,20,20). Фигурата, която описва кубчето при транслацията е фигурата в която трябва да се падне нашата точка.
Да, така е. Като тръгнах да го чертая стана.
Един човек да се срещне сам е 100% сигурно т.е. 4/4; 2ма човека да се срещнат е 7/16; 3ма да се срещнат е 10/64. От това заключавам, че формулата е (3n+1)/4n
superscript-а ми май не проработи
Интересно е като хипотеза... може би с компютърна програма може да се провери. Поне ще знаем какво да се опитваме да доказваме :)
става въпрос за 4^n, а не 4n
Оправих го.