C, PHP, VB, .NET

Обратните функции са симетрични на нормалните спрямо ъглополовящата на първи квадрант. Обратната функция трябва да приема всички стойности на оригиналната и да ги приема само веднъж. Един хубав тест дали една функция е обратима е "правилото на хоризонталната права". Ако придвижите една успоредна на остта x права от долу нагоре по остта y, то във всеки един момент тя трябва да пресича графиката на функцията само в една точка. Ако тя я пресича в две или повече, то функцията няма обратна функция. Например x^2 няма обратна функция.

Въпреки това ние сме приели да има обратни фунции на някои, които очевидно не са обратими. Например ние често казваме, че "обратната функция на sin(x) е arcsin(x)". Това всъщност се получава като "отрежем" само част от графиката на функцията sin(x) и по-точно - един неин период. На така получената функция ние намираме обратна и я кръщаваме "arcsin(x)". По същия начин постъпваме и при намирането на обратната функция на x^2 - там избираме само интервала x>=0 (понеже x^2 е симетрична спрямо остта y) и после обикновено казваме, че "обратната функция на x^2 е коренквадратен от x". По-долу обаче ще покажа, че това е напълно погрешно.

Днес в един от най-често посещаваните от мен блогове - този на Мъри Борн - попаднах на статия с много добро попадение свързано с функцията arccotg(x). В нея Мъри разглежда две възможни интерпретации на графичното изобразяване на функцията при различен избор на интервал. Едното е в интервала (-π/2,π/2), а другата е в интервал (0,π):

 

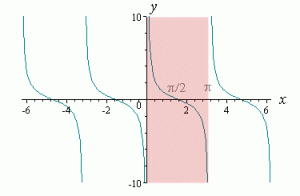
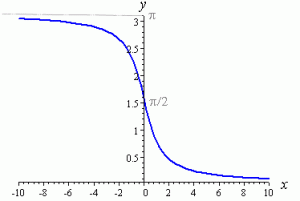
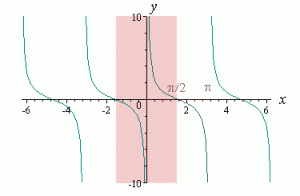
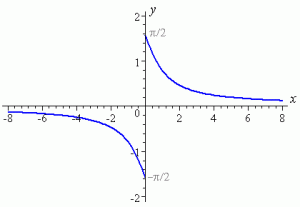
Естествено от тук следва нещо критично - изборът на интервал е много важен за получения резултат. В първия вариант arccotg(−2) = 2.678..., а във втория arccotg(−2) = −0.46365... Естествено ще си кажем, че не може и двете да са вярни, нали? А ако едното е грешно, то кое от тях?

Ако не желаете да мислите математически и се опитате да се допитате до големите софтуерни продукти (нали са големи, трябва да казват вярни неща, а?), то объркването ще стане още по-фрапиращо. MathCAD и Mapple ще ви покажат първата интерпретация, а Mathematica (WolframAlpha) и Mathlab ще ви покажат втората. Значи различен софтуер ще показва различни резултати при подаване на стойности на една и съща функция. Какво става?

Има една очевидна причина за избор на интервал (0,π). Има една теорема, която гласи, че ако една функция е монотонно растяща или монотонно намаляваща в даден интервал, то тя е обратима в него. Това е достатъчно условие за обратимост. Ами arctg(x) е монотонно растяща в (-π/2,π/2), а arccotg(x) е монотонно намаляваща в (0,π). Затова и всички учебници, които съм виждал избират именно тези интервали за обратните тригонометрични функции на тангенс и котангенс без особено замисляне - няма логическа причина дори да се помисли за избор на други.

И все пак - втората интерпретация също е валидна. Има обаче проблем в прекъснатостта - функцията arccos(x) не е дефинирана в x=0 ако сме избрали интервал (-π/2,π/2). Тоест реално интервала за дефиниране трябва да е  (-π/2,0)U(0,π/2). Но това всъщност не е проблем. Наистина не е логичен избор (при положение, че имаме друг претендент, в който cotg(x) е монотонно намаляваща), но за сметка на това НЕ нарушава условията за обратна функция.

Кое от двете е вярно ли? Отговорът на този казус е, че и двете интерпретации са вярни! Затова когато представяте сметки свързани с обратните функции, то е задължително да изписвате интервала, в който сте ги дефинирали. По същия начин, по който изписвате дефиниционното множество на нормалните функции. Спазването на това е задължително. Както виждате arccotg(x) в (-π/2,0)U(0,π/2) и arccotg(x) в (0,π) са обратните функции на две различни функции.

Така всъщност изказването, че "обратната функция на sin(x) е arcsin(x)" е напълно погрешно! Правилно е да кажем "обратната функция на sin(x) в интервала (-π/2,π/2) e arcsin(x)". По същия начин не е правилно да казваме, че "обратната функция на x^2 е коренквадратен от x" - правилното изказване е "обратната функция на [x^2 за x>=0 И недефинирана за x<0] е коренквадратен от x".

П.П. Има една друга закачка в статията - задава се въпроса "кое е правилното означение arccot(x) или acot(x)"? Аз казвам смело трети вариант - arccotg(x)!

Приели сме да пишем sin(x) и arcsin(x). Съответно cos(x) и arccos(x). Това е широко приета конвенция. Сега имаме tg (TanGent). Добавяме едно "co" за да получим cotg (COTanGent) и накрая "arc" за arccotg (ARCusCOTanGent).

Не виждам добра логика да изписваме котангенс като "cot". Обратната логика ще трябва да ни изведе до това да изписваме тангес само като "t", а това не е добре. Изглежда обаче западната литература е наложила точно тази антилогика - тангенс tg, а котангенс cot. По същия начин, по който противно на логиката на някои места е избран интервал (-π/2,0)U(0,π/2) за arccotg(x), вместо (0,π) :) :) :)