* Реални корени на биквадратно уравнение с a=1
Публикувано на 14 ноември 2012 в раздел Вероятности.
Задача. Дадено е биквадратното уравнение x4 + bx2 + c = 0. Каква е вероятността четирите му корена да са реални числа, ако b и c са в интервала [-n,n]?
Решение: Полагаме x2 = y. Получаваме квадратно уравнение y2 + by + c = 0.
Ако корените на това квадратно уравнение са комплексни числа, то и корените на биквадратното уравнение ще са комплексни. Така, че първото условие, което искаме да бъде изпълнено е корените на квадратното уравнение да са реални числа, т.е. D=b2-4c>0
Това обаче не е достатъчно. Ако някой корен измежду y1 или y2 е отрицателен, то съответните им корени на биквадратното уравнение x11, x12 или x21, x22 ще станат комплексни числа.
Така получаваме още две условия - y1>0 и y2>0
Тук на помощ ни идват формулите на Виет. Действително, ако y1>0 и y2>0 е изпълнено, то ще имаме
1) y1+y2 = -b/a = -b>0
2) y1y2 = c/a = c >0
Тоест двете условия се трансформират в условията b<0 и c>0.
Нека моделираме решението както в предишната задача. Там по оста x нанасяхме числата b, а по оста y числата c. Графиката на функцията b2-4c=0 отсичаше една парабола и решенията бяха под нея. Новите две условия 1) и 2) дефинират квадрант №2. Тоест трябва ни само областта под параболата във втори квадрант. Това се вижда и от графиката на функциите:
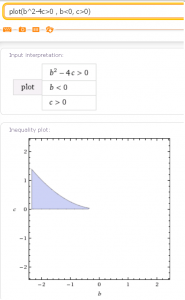 Остава да намерите лицето на защрихованата област и да го разделите на общото лице на квадрата. Не забравяйте да отчетете и стойностите на n в случаите n<4 или n>4. Направете го.
Остава да намерите лицето на защрихованата област и да го разделите на общото лице на квадрата. Не забравяйте да отчетете и стойностите на n в случаите n<4 или n>4. Направете го.
(3n - 4sqrt(n))/3n при n>4
n/12 при n<=4
П.п. малкo прибързан отговор. Изчислих направо вероятността. За лицето, съответният отговор да се умножи по n^2
Малко го пиша "на сляпо" и не съм убеден, че е вярно, но:
n<4:
[math]S(blue)=int_{-n}^{0}\frac{x^2}{4}dx=\frac{n^3}{12}[/math]
[math]S(all)=4n^2[/math]
=> [math]P=\frac{n^3}{4.12.n^2}=\frac{n}{48}[/math]
n>4:
[math]S(blue)=\int_{-2\sqrt{n}}^{0}\frac{x^2}{4}dx + (n-2\sqrt{n}).n=n^2-\frac{4.n^{3/2}}{3}[/math]
[math]S(all) = 4n^2[/math]
=> [math]P=\frac{n^2-\frac{4.n^{3/2}}{3}}{4n^2}=\frac{3n^2-4.n^{3/2}}{12n^2}=\frac{1}{4}-\frac{1}{3\sqrt{n}}[/math]
Да, моя грешка. Лицето на квадрата е 4n^2, а не n^2.
Интересното в този случай е, че при n клонящо към безкрайност, вероятността клони към точно P=1/4
Това се покрива и с извода от предишната задача за квадратните уравнения. Там вероятността клонеше към 1, т.е. благоприятните изходи имаха тенденция да покрива цялото пространство от четири квадранта. Тук има тенденция да се покриват все повече и повече от само един от четирите квадранта (2ри). Значи вероятността е четири пъти по-малка.
Сметките ми от предишния коментар изглеждат да са вярни.