* Магическото колело
Публикувано на 30 април 2009 в раздел Математика.
Колелото на картинката по-долу е магическо!
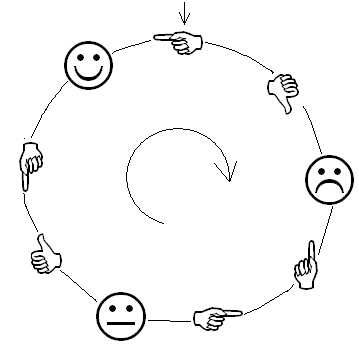
Ще ви го докажа. Намислете си едно положително цяло число. Може да е всякакво произволно число - дори много голямо - важното е да бъде положително. Например - вземете вашия телефонен номер (аз не го знам, т.е. за магическото колело той е напълно произволен).
Сега разместете цифрите на вашия телефонен номер както си искате. Например моят телефонен номер е 0893690135 и аз разместих цифрите му като 1593600938.
Сега от по-голямото число извадете по-малкото (1593600938 - 893690135 = 699910803). Започнете да броите по картинките в кръг започвайки от ръчичката сочеща наляво по посока на часовниковата стрелка. Например ръчичката сочеща наляво е 1, палецът сочещ надолу е 2, намусеното личице е 3, и т.н. Аз съм убеден, че когато стигнете до получената разлика (от примера 699910803), то вашият пръст ще бъде точно върху усмихнатото личице!
Тъй като вашия телефонен номер е прекалено голям и знам, че няма да ви се брои до толкова - пробвайте с някое по-малко произволно число. Всяко двуцифрено число ще свърши чудесна работа.
П.С. Естествено математиците или тези от вас, които са пробвали няколко пъти ще се досетят, че има един частен случай, когато разликата е 0. Получава се когато всички цифри на вашето число са еднакви, числото е едноцифрено или не сте размествали нищо. Е, в този случай отново попадате върху усмихнатото личице - ръчичката сочеща наляво е числото 1, т.е. вие ще трябва да се върнете с 1 назад за да достигнете до сума 0 :)
сега остава някой да обясни защо разликата на двете числа винаги е кратна на 9.
asd - Да, точно това трябва да се докаже :)
Понеже 9 е най-голямата цифра в десетичната бройна система, то всяко число е “сравнимо по модул 9″ със сумата от цифрите на самото число. Например остатъкът от делението на 41561 с 9 е 8. Сумата от цифрите на 41561 е 17, което от своя страна също дава остатък 8 при деление с 9. Още повече - сумата от цифрите на 17 е 8, което също дава остатък 8 при деление на 9.
Това всъщност сме го учили всички в училище - признакът на деление на едно число на 3 е сборът от цифрите на числото да се дели на 3. По този начин се стига и до признакът за деление на 9 - 9 = 3×3 => сборът от цифрите на числото трябва да се дели два пъти на 3, т.е. на 9.
Е, в тази задача се използва точно този “метод на задраскване на деветките”. Караме ви да намерите разликата между две числа, които са сравними и така да се каже се “убива” остатъка от деление на девет (самото въртене по колелото се явява премахване на деветки) и ни оставя число кратно на 9.
Нека първото число е Y1 = X1 + k, където k е остатъкът от деление на Y1 с 9. Нека второто число е Y2 = X2 + k (Y1 и Y2 са сравними, защото сборът от цифрите им е еднакъв т.е. дават един и същи остатък при деление с 9). Отбелязваме, че в случая X1 и X2 са числа кратни на 9! Разликата на двете числа е:
Y1 - Y2 = X1 + k - X2 - k = X1 - X2.
Остава да се докаже, че разликата на две числа X1 и X2, които са делими на 9, е число, което също е делимо на 9. Това ще оставя на вас :)
Да бе не е магически този кръг!Не е честно!Това е тъпо!Адски тъпо!