* Задача за пермутации
Публикувано на 09 май 2009 в раздел Математика.
Реших да си припомня малко от скромните си познания по комбинаторика. Стигнах до една изключително приятна задача за упражнение, която разширих значително:
Нека имаме 5 плода и 8 деца. По колко различни начина можете да дадете плодовете на децата, ако:
а) Плодовете са различни, децата са различни (между тях няма еднояйчни близнаци) и всяко дете може да вземе всяко възможно количество плодове;
б) Плодовете са различни, децата са различни и едно дете не може да вземе повече от един плод;
в) Плодовете са еднакви, децата са различни и всяко дете може да вземе максимално по един плод;
г) Плодовете са еднакви и децата са еднакви (по някакъв странен природен феномен са се родили 8 еднояйчни близнаци, които не можем да различим един от друг по никакъв начин), като всяко дете може да вземе не повече от един плод;
д) Отново децата са напълно еднакви и могат да вземат максимум по един плод, но този път плодовете са различни;
е) Плодовете са различни, 6 от децата са различни, а две от тях са от въпросните неразличими близнаци. Всяко дете може да вземе не повече от един плод;
ж) Плодовете са две ябълки, една круша, едно манго и един банан, 6 от децата са различни и две са еднакви, като всяко дете може да вземе максимум по една ябълка;
з) Плодовете са две ябълки, една круша, едно манго и един банан, 6 от децата са различни и две са еднакви, като всяко дете може да вземе всяко възможно количество плодове;
и) Плодовете са две ябълки, една круша, едно манго и един банан, 6 от децата са различни и две са еднакви, като всяко дете може да вземе не повече от два плода;
Мисля, че вариантите са достатъчно. Моля всички хора, които са близнаци да не се обиждат от условието на задачата - направена е така само и единствено с образователна цел.
А сега, след като сте подготвили комбинаторното си мислене добре, нещо много по-интересно. Един приятел ми изпрати следната картинка:
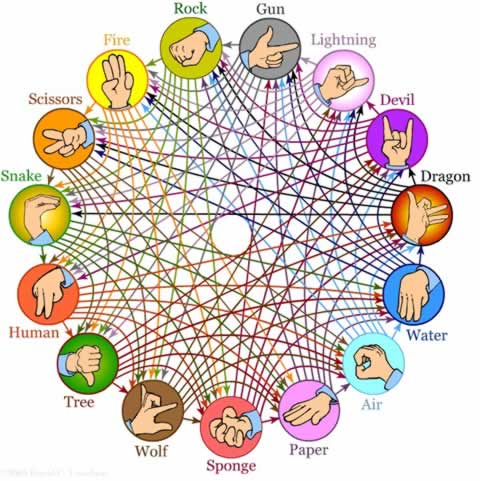
За съжаление не познавам авторът, но това е очевидно играта камък-ножица-хартия във вариант с 15 възможни хода. Виждате, че са показани всички възможни комбинации между тях. Предлагам да станем професионални играчи и да си организираме турнир :)
Искам и аз да дам една задача (примерна) с цели числа. Поискали на един човек в България джиесем номера за връзка. Той отговорил:
-Ако ми умножите моето ICQ със числото 45.7643837427670147245982462886 ще се получи номера ми (ще сложите и една нула отпред, знаете че номерата имат още 9 цифри, може да използвате и това, че започват с 8 - само за българите един хинт в повече).
Може ли да разберете номера му? Примера ми има решение!
Отбивате темата в страни. Тук говорим за комбинаторика. Ето решенията на няколко от задачите:
1. За всеки един плод има по 8 възможни деца за комбинация, т.е. отговорът е 5^8 или 32768 комбинации.
2. Първият плод може да бъде даден на общо 8 деца, вторият плод на 7, третият на 6, четвъртият на 5 и петият на 4 => отговорът е 8.7.6.5.4 = 6720 комбинации.
3. Тъй като плодовете са еднакви, а децата различни, то ни трябват възможните комбинации между децата:
1ва комбинация: първото, второто, третото, четвъртото и петото взимат плод, а другите не.
2ра комбинация: първото, второто, третото, четвъртото и шестото взимат плод, а другите не.
...
Лесно се пресмята, че отговорът е 56. Пет комбинации над осем елемента се смята по следната формула:
C(8,5) = 8! / 5!.(8-5)! = 40320 / 120 . 6 = 56...
Аз с лесните съм дотук. Останалите отговори ги давам на вас...
Lesna Rabota, тази астрономическа точност с windows calculator ли я постигна? Какво ще ми дадеш ако реша задачата?
Защо да ти давам нещо, Мими? -Аз си знам отговора:-)
Хайде още малко помощ:
4. Щом и плодовете са еднакви и децата са еднакви, то има само една възможна комбинация.
5. Плодовете са различни, но децата са еднакви - тук много хора се заблуждават. Има само една възможна комбинация и тя е да дадете по един плод на което и да е дете. Тук задачата се гледа на обратно - всъщност вие "давате дете на плод". Тъй като децата са повече от плодовете, то всеки плод ще си има по едно детенце винаги, а те са еднакви, т.е. имаме само една възможна комбинация...
От тук нататък вече не казвам!