* Раздробената окръжност
Публикувано на 29 ноември 2010 в раздел Математика.
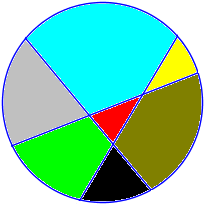
Можете ли да „разрежете“ окръжност с три прави линии така, че окръжността да се „начупи“ на седем (7) парчета, като всички парчета са с равни лица?
Примерно разделяне на седем части, което НЕ е решение
Според мен няма решение. Единствения начин, вобще да има 7 части е линиите да се пресичат така както е показано на примера – да заключват триъгълник в центъра. Да разгледаме частта която включва черното, кафявото и жълтото парче. Единствения начин тези парчета да са с равни лица по между си е, дргите линии да се пресичат в една точка и да разделят 180 градуса на 3 равни ъгъла. Но тъй като за да съществува червения триъгълник (трябва да има страна) е нужно двете прави да не се пресичат в една точка. Това е в противоречие с по-горното заключение и следователно задачата няма решение.
И аз мисля така. Не съм пробвал да го докажа строго, но пробвах с динамичен софтуер за геометрия. Не се получава :)
Първо делкате с една линия- тя трябва да дели в съотношение 4:3 или 5:2 или 6:1, ама реално става само с 4:3, т.е. дотук един вариант. Нататък намерете решение за втората линия която да раздели на 2:1:2:2 и тогава ми се обадете – аз ще помисля за третата :-)
Трябва ВСЯКА ЛИНИЯ да дели окръжността в съотношение 4-3. Логично за да стане евентулно нещо, трябва трите линии да са под 60 градуса (по Целзий) една спрямо друга. Така ще се получат две тройки еднакви области и една средна (като червената горе, която е като банския ми), тоест три размера, които ако са равни -ок, ама надали.
Филипе, ако сметнеш в какво съотношение са седемте области x+x+x+y+y+y+z=1, ще ти покажа нещо.
Първото ти изречение е вярно на 100%. А градусите може и да са по Фаренхайт, може и да са алкохолни. Да те черпя нещо?
Че задачата няма решение – няма… Но за съжаление трябва да се докаже. Това са най-трудните задачи :)
Мими, Мимиии, Мими,
Задачата няма решение. Ако разделим кръга така както предлагаш ти, ще получим (горе долу) следнато:
http://dl.dropbox.com/u/5859896/sample.bmp
(2X+Y+Z):(2Y+X)=4:3
Жестоко… но това по никакъв начин не значи че X=Y=Z. Пример:
X=0.5 Y=1.25 Z=1.75
(2*0.5+1.25+1.75):(0.5+2*1.25)=4:3
Наздраве!
1. Трябва да се докаже, че това е единствената конфигурация, в която окръжността може да се раздели на 7 части;
2. Не ми стана ясно защо „всички прави взаимно се делят в отношение 1:2“. А на графиката отсечка „x“ мая няма. Но иначе видях логиката на решението – изглежда вярна.
Добре де Филка,
Нека изпипаме нещата. Доказателството не е елегатно, но все пак:
Фигура: http://dl.dropbox.com/u/5859896/sample2.bmp
1.Да допуснем, че съществува такова разделение!
2.Тогава Y:(Z+X)=1:2 => всички прави взаимно се делят в отношение 1:2 => (отсечките) x=y => правите се пресичат под ъгъл 60 градуса.
3.От 2 => триъгълниците Z и Y-T имат равни лица: Z=Y-T, но от 1 => Z=Y
Е стигнахме до противоречие, следователно допускането, че съществува такова разделение е грешно.