* Три успоредни линии и равностранен триъгълник
Публикувано на 17 януари 2009 в раздел Математика.
Това е интересна построителна задача, която първоначално ме затрудни доста.
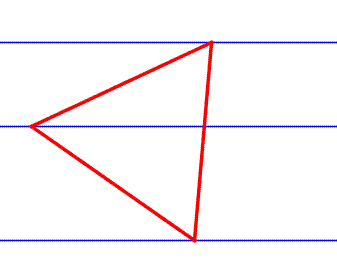
Задачата е следната: Дадени са три успоредни линии. Постройте равностранен триъгълник, чиито върхове лежат на всяка една от линиите.
Припомням, че трябва да разгледате всички възможни разположения на линиите. Може да използвате Geonext или Geogebra за удобство.
Разстоянието между горната и средната линия е A, а между средната и долната B.
Започвам да строя така. Произволна точка върху средната права, все отнякъде се започва. Чертая линия, наклонена под ъгъл E надясно и нагоре, докато стигна горната линия и това е едната страна на триъгълника с дължина L. Другото е лесно. Сега остава да кажа колко е ъгъл E.
Елементарно се установява, че:
A/sinE = B/sin(60-E)
защото L=A/sinE = B/sin(60-E)
заб.
Мисля, че не е трудно да се реши уравнението, но от 10 години не съм решавал тригонометричните, едно време бях мастер на тях. Май първо трябва да се ползва формулата за sin(60-E)=sin60.cosE-cos60.sinE, която сигурно не съм я написал правилно, но ме мързи да я търся в един справочник на Ханс Йохен Барч, май.
Ще те помъча малко - трябва да се направи и анализ за брой различни решения при един фиксиран връх за различните разположения на правите (те може дори да съвпадат)... :)