C, PHP, VB, .NET

Основно понятие при обработката на информация е алгоритъм. Всички изчисления в една компютърна програма се правят по предварително определени правила. Съвкупност от логически свързани правила ще наричаме алгоритъм. Като формална дефиниция ще приемем следната:

Деф. Алгоритъм наричаме система от правила, които определят последователност от изчислителни операции, прилагането на които води до решението на дадена задача.

Основните компоненти за всеки алгоритъм са три:

• Входни данни: това е информацията, която се приема за даденост на алгоритъма. В програмирането това обикновено са някакви величини - константи или променливи;
• Тяло на алгоритъма: изпълним програмен код, който извършва обработка на информацията;
• Изходни данни: резултатът от алгоритъма, който може да се използва от човек или от други алгоритми.

Най-простият начин за описание на алгоритмите, който е и най-близък до естественото възприятие на човека, е "словесен" (с думи). Например нека имаме следната задача:

Задача 1. Дадена е поредица от числа a₁, a₂, a₃, ..., a_n. Намерете най-малкото число в поредицата.

В тази задача входните данни са съответната поредица от числа. Те не са дадени строго фиксирани (с конкретни стойности), а като променливи величини. Очакваните изходни данни са едно число - най-малкото от подадените.

Как решавате тази задача, ако ви бъде дадена на лист хартия? Естествено, че вие оглеждате последователно числата и в даден момент помните само текущо най-малкото такова - ако забележите друго число, което е по-малко от досега помненото, вие ще забравите старото и ще запомните новото. След като прегледате всички числа, вие съобщавате последното запомнено число като решение на задачата.

Когато трябва да прехвърлим отговорността за решението на подобна задача на компютър, ние трябва да го разбием на краен брой елементарни изчислителни операции. Ето как може да стане това:

1. Резервирайте място, където да запазим решението на задачата - нека това място е "R". Премини на 2;
2. Резервирайте място за пореден индекс на число в редицата - нека това място е "k". Премини на 3
3. Запишете R=a₁. Премини на 4;
4. Запишете k=1. Премини на 5;
5. Увеличете k с 1 и проверете: ако R<=a_k, премини на 6, а ако R>a_k, премини на 7;
6. Проверетe: ако k=n, премини на 8. Ако k<n, премини на 5;
7. Запишете R=a_k. Премини на 6;
8. Решението ѝ е запазено в R. Край.

Виждате, че всяка стъпка от извършването на алгоритъма има три основни компонента:

• Номер на стъпката;
• Действие, което ще се изпълни;
• Номер на следваща стъпка, в която да се отиде, в зависимост от извършеното действие.

Действията от своя страна са два вида:

• Безусловни: като следствие от тях се отива на една точно определена стъпка. От примера това са действията извършени в 1, 2, 3, 4 и 7;
• Условни: в зависимост от резултат от логически оператор се отива на една от две възможни следващи стъпки. От примера това са действията в 5 и 6.

Нещо, което може да забележите от примера, е че поредица от стъпки в даден алгоритъм може да се повтаря многократно, т.е. да образува цикъл. Комбинацията от стъпки 5, 6 и 7 в примера са именно такъв цикъл. Ако от даден цикъл никога не се достига до изход (повтаря се до безкрайност), ще го наричаме "безкраен цикъл", а ако има - "краен".

Ако при едни и същи входни данни даден алгоритъм дава един и същи краен резултат (изход), ще казваме, че алгоритъма е детерминистичен. Ако при едни и същи входни данни се получава различен резултат, ще казваме, че е недетерминистичен. Недетерминистичен алгоритъм може да се получи например при използване на действие, в което се генерира произволно число.

Нека разгледаме няколко примера за алгоритми.

Задача 2. Въведете три числа a, b и c, след което изчислете и отпечатайте на екрана периметъра на триъгълник със страни с дължини a, b и c.

Решение: В този алгоритъм нямаме входни данни. Извършваме следните стъпки:

1. Въведи стойност в променливата a. Премини на 2;
2. Въведи стойност в променливата b. Премини на 3;
3. Въведи стойност в променливата c. Премини на 4;
4. Провери дали е вярно условието "(a+b>c) AND (a+c>b) AND (b+c>a)". Ако е вярно, премини на 6. Ако не е вярно, премини на 5;
5. Изведи на екрана "такъв триъгълник не може да съществува" и прекрати програмата. Край;
6. Резервирайте място, където да запазим решението на задачата - нека това място е "R". Премини на 7;
7. Запишете R = a+b+c. Премини на 8;
8. Изведи R на екрана на компютъра. Край.

Виждате, че в този алгоритъм имаме две различни стъпки, в които можем да достигнем до изходна точка.

Задача 3. По подадени две числа "a" и "b", намерете техния НОД по алгоритъм на Евклид.

Решение:

1. Провери дали a>b. Ако това е вярно, премини на стъпка 2. Ако това не е вярно, премини на стъпка 3;
2. Променете a=a-b. Премини на стъпка 1;
3. Провери дали a<b. Ако това е вярно, премини на стъпка 4. Ако това не е вярно, премини на стъпка 5;
4. Променете b=b-a. Премини на стъпка 1;
5. Стойността на "a" е търсения резултат. Край.

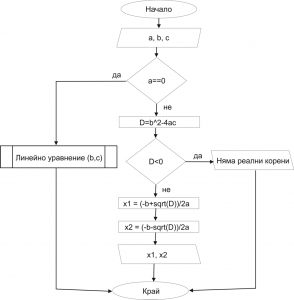
Задача 4. По подадени три числа "a", "b" и "c", намерете корените на квадратно уравнение y=ax²+bx+c.

Решение: С цел да опростим

1. Провери дали a==0. Ако е вярно, премини на 11. Ако не е вярно, премини на 2;
2. Запазете място за дискриминантата D. Премини на стъпка 3;
3. Запишете D=b²-4ac. Премини на стъпка 4;
4. Провери дали дискриминантата D<0. Ако е вярно, премини на 5. Ако не е вярно, премини на 6;
5. Изведи решение, че няма реални корени. Край;
6. Запазете място за корена x₁. Премини на 7;
7. Запишете x₁=(-b+sqrt(D))/2a. Премини на 8;
8. Запазете място за корена x₂. Премини на 9;
9. Запишете x₂=(-b-sqrt(D))/2a. Премини на 10;
10. Изведете на екрана в подходящ вид стойностите на x₁ и x₂. Край.
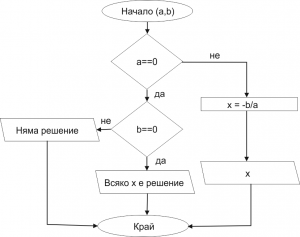
11. Провери дали b==0. Ако е вярно, премини на 15. Ако не е вярно, премини на 12.
12. Запазете място за корена x. Премини на 13.
13. Запишете x=-b/a. Премини на 14
14. Изведете на екрана в подходящ вид стойността на x. Край.
15. Провери дали c==0. Ако е вярно, премини на 16. Ако не е вярно, премини на 17.
16. Изведете на екрана "всяко x е решение". Край.
17. Изведете на екрана "няма решение". Край.

На теория всяка една компютърна програма, независимо колко сложна е тя, може да бъде описана по този начин. Естествено това не е най-практичното решение. Например би било много по-лесно да представим изходите от условните действия във вид на разклонен граф, вместо както е в случая - линейно. За тази цел, както и за други чисто визуални улеснения, е прието алгоритмите да се представят чрез т.нар. "блок-схеми". Те се състоят от следните компоненти:

• Начало и край на алгоритъма:
  
• Безусловни действия:
  
• Условни действия:
  
• Въвеждане на данни (заделяне на пространство за тях и прочитането им от входно устройство, например клавиатура, скенер, файл, фотоапарат, камера и др.):
  
• Изход (предаване на данни към изходно устройство, например печатане на екран, принтер, запазване във файл и др.):
  
• Подалгоритми (възможност за вграждане на цяла блок-схема вътре в друга блок-схема):
  

Нека покажем как ще изглежда една примерна задача.

Задача 5. По подадени две числа "a" и "b" намерете решението на линейното уравнение ax+b=0

Решение:

 

Задача 6. Въведете три числа "a", "b" и "c". Намереше решение на квадратното уравнение ax^2+bx+c=0

Решение: Вече знаейки как се решава линейно уравнение, ние ще го използваме като подалгоритъм, а няма да го решаваме наново:

Допълнителни задачи:

1. Направете блок-схеми на задачи 1, 2, 3 и 4 и направете словесното решение на задача 5.

2.  Компютърът си намисля произволно число N в интервала [1, 512]. Имате право да налучквате най-много 9 пъти. При всеки неуспешен опит компютърът ще ви казва дали „числото е по-малко“ или „числото е по-голямо“ от намисленото. Ако налучкате числото, на екрана се появява надпис „Успя“. Ако не успеете да налучкате числото, на екрана се появява надпис „Загуби“.

а) Начертайте блок-схема на алгоритъма;

б) Реализирайте алгоритъма на програмен език по ваш избор;

в) Измислете тактика, чрез която винаги да печелите играта.

3. Дадено е моментното състояние на играта XO в таблица с размери 3х3. Ако в дадена клетка не е играно, в нея ще записано числото 0, ако е играно с Х, ще е записано числото 1, а ако е играно O, ще е записано числото 2. Например:

Примерни данни

1	0	1
1	2	0
2	0	0

=>

Реална игра

X		X
X	O
O

Играчите играят последователно слагайки символите Х и О в таблицата. За победител се счита този, който успее да нареди три пъти своя символ един до друг по хоризонтала, вертикала или диагонал.

а) Направете блок-схема на алгоритъм, в който по подадена таблица и символ („Х“ или „О“), се проверява дали подадения символ е победител в играта;

б) Реализирайте алгоритъма на програмен език по ваш избор.

4. John се катери към върха на планината. Остават му пет крачки до целта. За нещастие на други пет крачки в обратна посока е пропастта, в която го чака алтернативен край на неговото пътешествие.

Трябва да напишем интерактивна програма за деца, при която е имплементирана следната логика (последователност от стъпки):

• Компютъра си намисля две произволни цели числа A и B в интервала [0, 20], и произволна математическа операция OP измежду четирите: +, -, * и /.
• Ако операцията е “/”, трябва да се провери дали A се дели на B без остатък (т.е. дали A%B==0). Ако това е вярно, продължавате напред. Ако не е вярно, генерираме ново произволно B отново и отново, докато намерим такова B, което да дели А. Внимание: тук се пазим също от случая, в който делим на нула – ако това се случи, планината ще се срути от гигантско земетресение, т.е. нещо, което не желаем да се случва и трябва на всяка цена да предотвратим;
• На екрана се отпечатва “A OP B = ?” (например при A=12, B=9 и OP=+ ще се изпише “12 + 9 = ?”);
• Потребителят въвежда от клавиатурата отговор. Ако този отговор е верен, John ще направи стъпка напред. Ако отговорът не е верен, John ще направи стъпка назад. След това всичко продължава отначало първото тире, в което компютъра отново намисля математически израз;
• Играта продължава дотогава, докато John достигне върха или пропадне в пропастта.

а) Поправете описанието от по-горе така, че да стане завършен алгоритъм с валидно словесно описание;

б) Направете блок-схема на играта и я реализирайте на език за програмиране по ваш избор.

5. В следния код написан на Java е реализирана играта „бесеница“.

import java.util.Scanner;
public class WordGuess{
  static String word = "Pandemonium";
  static final int MAXWRONGS = 6;
  
  public static void main(String[] args){
    
    char[] dashes = new char[word.length()];
    for(int i=0; i<word.length(); i++){
      dashes[i] = '-';
    }
    Scanner keybIn = new Scanner(System.in);
    
    int wrongs = 0;
    while(wrongs<MAXWRONGS && !wordIsGuessed(dashes)){
      printStatus(dashes);
      System.out.print("Подайте буква: ");
      char c = keybIn.nextLine().charAt(0);
      int fount = word.indexOf(c);
      if(fount == -1){
        System.out.println("Съжалявам, не го намерих.");
        wrongs++;
      }
      else{
        System.out.println("ДА, има я!");
        revealLetter(word, dashes, c);
      }
    }
    
    if(wrongs<6) System.out.println("Познахте! Думата е "+word);
    else System.out.println("Вие сте обесен!  Думата беше "+word);
  }
  
  public static void printStatus(char[] arr){
    for(char c: arr){
      System.out.print(c+" ");
    }
    System.out.println();
  }
  
  public static boolean wordIsGuessed(char[] dashes){
    for(char c: dashes){
      if(c=='-') return false;
    }
    return true;
  }
  
  public static void revealLetter(String word, char[] dashes, char letter){
    for (int i = 0; i < word.length(); i++){
      if (word.charAt(i) == letter){
        dashes[i] = letter;
      }
    }
  }
}

Свали сорс кода от тук.

Ако приемете, че статичните променливи “word” и “MAXWRONGS” са входни параметри за алгоритъма, направете блок-схема, която описва програмата.

Упътване: Ще бъде удачно методите printStatus, wordIsGuessed и revealLetter да бъдат реализирани като самостоятелни блок-схеми и да бъдат включени в голямата като подалгоритми.