C, PHP, VB, .NET

Обемът на едно понятие съдържа n-орки обекти, които могат да бъдат наредени или ненаредени. Обектите "обхванати" от едно понятие са обвързани чрез връзки помежду си. Например родствените връзки между майка, баща, син и дъщеря, които са подмножества на понятието "семейство".

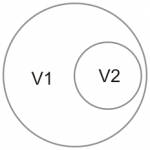
Когато едно понятие P1 с обем V1 съдържа в себе си всички свойства на понятие P2 с обем V2, то ще казваме, че P2 е подмножество на P1 и ще бележим, че V2 V1. Ще казваме, че P2 е видово на P1, а P1 е родово на P2. Например правоъгълникът е родов за квадрата, а квадратът е видов за правоъгълника.

Определенията и дефинициите обикновено следват последователността от род към вид. Това е съвсем нормално - обикновено дефинираме едно голямото множество (род), а след това разглеждаме конкретни негови частни случаи (видове). Например дефиницията "правоъгълникът е успоредник, чийто ъгли са прави" е точно такава. Вече сме дефинирали рода "успоредник" и чрез него определяме конкретен вид "правоъгълник".

Много по-рядко се вижда обратното - дефиниция от вид към род. Например дефиницията, че цилиндър може да се получи чрез въртене на правоъгълник около една от страните му. Това са нетраниционни дефиниции.

В миналата тема засегнах едно основно правило за дефиниция, а именно:

Всеки един обект или понятие трябва да бъде дефиниран
чрез използването на вече познати обекти и/или понятия!

Тук ще разширя правилата, като допълня с още:

1. При дефинициите не трябва да се получава цикличност, т.е. ако за дефинирането на понятие P1 използваме P2, за дефиниране на P2 използваме P3, а за дефиниране на P3 използваме P1. В още по-прост пример когато попитаме "какво е пръчка" да отговорим "парче дърво", а като попитаме "какво е парче дърво" да отговорим с "пръчка". Такива ситуации трябва да се избягват напълно;
2. При дефиницията да се използват минимално количество свойства на обекта, които са достатъчни да го определят напълно;
3. Ако имаме дефиниция от род към вид, то да използваме най-близкия до вида род.

Може би четейки основното правило за дефиниция вече съзряхте един голям проблем - щом за да дефинираме едно понятие трябва да използваме вече преди това дефинирани понятия, то не се ли получава безкрайност? Ами да, истината е, че се получава. За да дефинираме "ротвайлер" ние обясняваме, че това е порода куче. Преди това е трябвало да дефинираме "куче" и сме казали, че това е "бозайник" с определени характеристики. Така се налага да дефинираме "бозайник", "животно", "живо същество", "организъм", "многоклетъчно" и т.н. Ами помислете - всяка една дума, която използваме в дефиницията трябва да бъде позната, т.е. дефинирана. Не се ли получава парадокс?

Решението на този проблем идва по два начина. Ако обекта или понятието са реални, то крайната дефиниция е чрез директно посочване. Ако обекта или понятието са абстрактни, то се използват аксиоми. Понякога се налага да използваме и точно това, за което казах, че е вредно за обучението - догматичност. Все пак това е нужно, за да не изпадаме в безкрайни дефиниции. Важното е да сме достатъчно убедителни и да успеем да поставим нужния базис, който да бъде логично обоснован.

Често точно за тези цели се използва т.нар. пропедефтика. Това е похват, чрез който ние караме учениците да използват понятия без да знаят техния конкретен термин, т.е. все още не са строго дефинирани. Например в ранните класове ги караме да решават задачи от типа 2 + x = 8, но въобще не им споменаваме за понятието "корен на уравнението". Вместо това използваме определението "неизвестно" - то е по-близко до текущите разбирания на учениците.

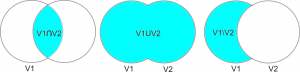
Накрая трябва да отбележим, че един обект или понятие може да участва като подмножество в повече от едно понятие. В такъв случай казваме, че имаме споделени множества. За да намираме общите елементи на две понятия P1 и P2 с обеми V1 и V2 използваме конюнкция и бележим с V1∩V2. За да обединим две понятия p1 и P2 с обеми V1 и V2 в едно общо понятие P3 с обем V3 използваме дизюнкция и бележим V3 = V1UV2. Ако изкаме да открием елементите на понятие P1 с обем V1, които не участват в понятие P2 с обем V2, то използваме разлика V1\V2. Следните графики демонстрират нагледно това, като сеченията са оцветени в синьо:

За конюнкцията и дизюнкзията трябва да знаем, че притежават комутативност и асоциативност, т.е.:

• V1UV2 = V2UV1 и  V1∩V2 = V2∩V1;

• (V1UV2)UV3 = V1U(V2UV3) и (V1∩V2)∩V3 = V1∩(V2∩V3).

Редно е да дам няколко примера. Предварително обаче искам да се застраховам, че  примерните ми дефиниции не са точни.

Пример за конюнкция: "Източно православни" (множество P1 с обем V1) наричаме християните (P2 с обем V2) от източна Европа (P3 с обем V3) => V1 = V2∩V3. Виждате, че конюнкцията се използва за дефиниции от род към вид.

Пример за дизюнкция: "Християни" (P1 с обем V1) наричаме множеството на католиците (P2 с обем V2), протестантите (P3 с обем V3) и източно православните (P4 с обем V4) => V1 = V1UV2UV3. Тук дефиницията е от вид към род.

Пример за подмножество: "Българо-мохамедани" (P1 с обем V1) наричаме българските граждани (p2 с обем V2), които изповядват исляма => V1 V2.

Пример за разлика: "Право да работят в полицията" (P1 с обем V1) имат тези хора (P2 с обем V2), които не са криминално проявени (P3 с обем V3) => V1 = V2\V3.

Специално внимание отбележете и на отрицанието. Всичко, което не попада в обема V1 на понятието P1, бележим с !V1:

Бъдете изключително внимателни с отрицанията - те обикновено объркват учениците. Избягвайте да работите с тях, когато това е възможно.