C, PHP, VB, .NET

Нека е даден квадрат [mathi]ABCD[/mathi] чиято страна е с дължина [mathi]a[/mathi]. Избираме произволна точка [mathi]P[/mathi] вътре в квадрата. Каква е вероятността [mathi]\triangle ABP[/mathi] да е тъпоъгълен?

Решение: Нека средата на [mathi]AB[/mathi] e точка [mathi]M[/mathi]. Построяваме окръжност с център [mathi]M[/mathi] и радиус [mathi]AM = \frac{a}{2}[/mathi]. Знаем, че ако т. [mathi]P[/mathi] лежи върху тази окръжност, [mathi]\angle APB=90^{\circ}[/mathi]. Ако точката е вътре в полуокръжността (оцветената в жълто част от чертежа), тогава триъгълника ще е тъпоъгълен.

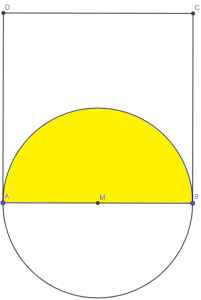
Оттук лесно можем да намерим търсената вероятност. Тя е:

[math]P(\angle APB>90^{\circ}) = \frac{S(полуокръжността)}{S(квадрата)}=\frac{\frac{\pi \times (\frac{a}{2})^2}{2}}{a^{2}}=\frac{\pi \times a^{2}}{8a^{2}}=\frac{\pi}{8}[/math]