* Положение на две точки върху отсечка
Публикувано на 06 февруари 2010 в раздел Вероятности.
Задача: Нека отсечката AB е с дължина l (|AB|=l) и нека точките M1∈AB и M2∈AB. Каква е вероятността |M1M2| ≤ k.l, където k e произволно число в интервала [0, 1]?
Решение: Нека |AM1| = x. Взимаме в ляво и в дясно от M1 точките C и D такива, че |CM1| = |M1D| = k.l. Да разгледаме два случая:
I случай. k≤½l
Тук имаме три възможни положения на точките:
a) 0< x < kl
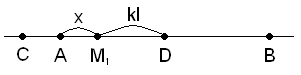
Тогава вероятността P(M1M2 ≤ k.l) съвпада с вероятността т.M2 ∈ AD и |AD| = x+kl
b) kl < x < l-kl
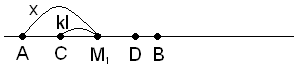
Тогава вероятността P(M1M2 ≤ k.l) съвпада с вероятността т.M2 ∈ CD и |CD| = 2kl
c) l-kl < x < l
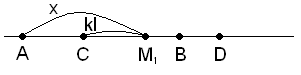 Тогава вероятността P(M1M2 ≤ k.l) съвпада с вероятността т.M2 ∈ CB и |CB| = l-x+kl
Тогава вероятността P(M1M2 ≤ k.l) съвпада с вероятността т.M2 ∈ CB и |CB| = l-x+kl
Общата вероятност от трите подслучая е:
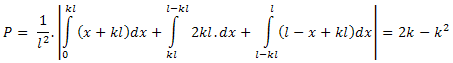
II случай: k > ½l
a) 0 < x < l-kl
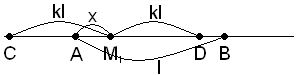
Тогава вероятността P(M1M2 ≤ k.l) съвпада с вероятността т.M2 ∈ AD и |AD| = x+kl
b) l-kl < x < l
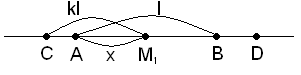
Тогава вероятността P(M1M2 ≤ k.l) съвпада с вероятността т.M2 ∈ AB и |AB| = l
c) kl < x < l
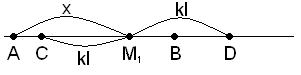 Тогава вероятността P(M1M2 ≤ k.l) съвпада с вероятността т.M2 ∈ CB и |CB| = l-x+kl
Тогава вероятността P(M1M2 ≤ k.l) съвпада с вероятността т.M2 ∈ CB и |CB| = l-x+kl
Общата вероятност от трите подслучая е:
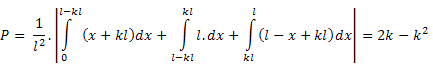
Тъй като и в Iсл и в IIсл вероятностите са едни и същи, то общо вероятността е:
P = 2k - k2
Средна стойност: Нека разгледаме и средната стойност на отсечката M1M2. Нека |AM1|=x и |AM2|=y. Тогава средната стойност е:
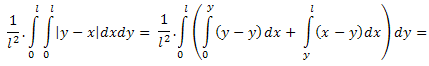
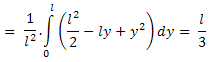
Добави коментар