C, PHP, VB, .NET

Задача: Нека имаме окръжност k с радиус 1 и две точки M₁∈k и M₂∈k. Каква е вероятността дъгата M₁M₂≤α<π?

Решение: Построяваме две точки C и D такива, че дъгите CM₁=α и M₁D=α:

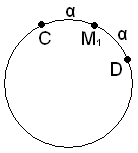Тогава вероятността дъгата M₁M₂≤α е равна на вероятността M₂ да принадлежи на дъгата CD. Дължината на дъгата CD е |CD|=2α

=> Търсената вероятност e:

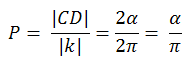Средна стойност: Елементарната вероятност е dα/π => средната стойност е:

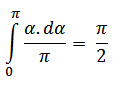
Задача за упражнение: Изведете по аналогия вероятността M₁M₂ да принадлежи на сегмент (кръг) с лице S₁ от сфера с лице S.