* Проблемът на Бюфон за иглата
Публикувано на 10 февруари 2010 в раздел Вероятности.
Задача: "Разграфяваме" равнината с успоредни линии на разстояние "2a" една от друга. Каква е вероятността произволно поставена отсечка с дължина "2l" да пресече някоя линия?
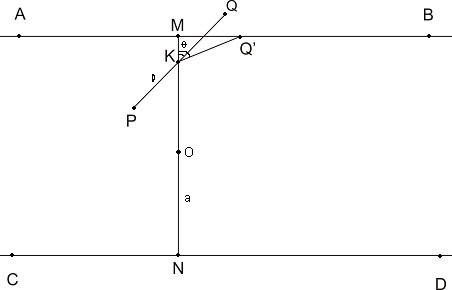
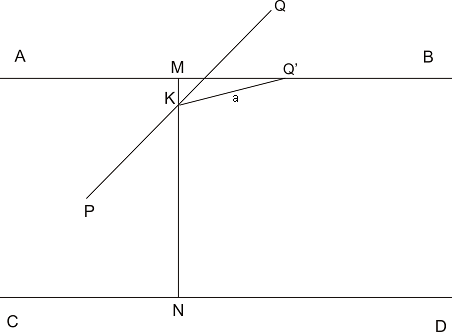
Решение: Взимаме две прави в равнината и на всяка от тях взимаме по две точки - A и B; C и D. Нека краищата на иглата са точките P и Q. Нека К е центъра на PQ и нека точките M и N принадлежат на правите като отсечката MN минава през K и е перпендикулярна на правите. Ще отбележим дължината на отсечката |MK| = x.
1 сл. l<a). Без да ограничаваме общността приемаме, че K е по-близко до АB отколкото до CD или по средата на MN.
За да пресича AB отсечката PQ трябва ъгъл <QKM да бъде по-малък от <Q'KM = θ, където |Q'K| = l.
=>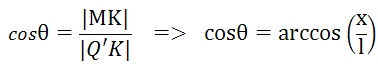
Вероятността на ъгъл <QKM да бъде по-малък от <Q'KM е θ/(π/2) = 2θ/π
=>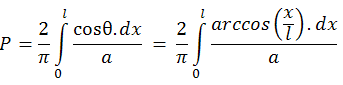 Полагаме x = lt
Полагаме x = lt
=> 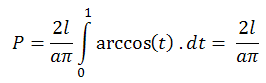
2сл. l>a) Отново PQ ще пресече по-близката ѝ до центъра K права. Отново без ограничение на общността приемаме, че K лежи върху отсечката MO. Имаме абсолютно същата ситуация както в миналата задача, но този път |Q'K|=a:
Така само ще се измени горната граница на интеграла:
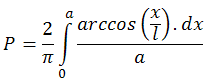
Ако a=l.cos(α) и положим x=l.cos(t) => dx=-l.sin(t).dt
=>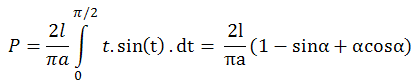 =>
=> 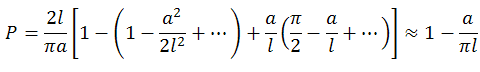
Добави коментар