* Проблемът на Лаплас за иглата
Публикувано на 23 февруари 2010 в раздел Вероятности.
Задача: В равнината е построена мрежа от правоъгълници със страни a и b. Каква е вероятността отсечка с дължина l да пресече страна на някой от правоъгълниците?
Решение: Нека l<a и l<b. Разглеждаме правоъгълник OABC. Произволна отсечка e PQ с дължина l и нейния център е т.K. Избираме координатна система с център т.O и оси OA и OC.
Нека отсечка PQ сключва ъгъл Θ с оста Ox. В правоъгълника OABC вписваме правоъгълник O'A'B'C' такъв, че:
- |OO'| = |AA'| = |BB'| = |CC'| = l/2
- Ъгъл <O'OA = <AA'O = <C'CB = <B'BC = Θ.
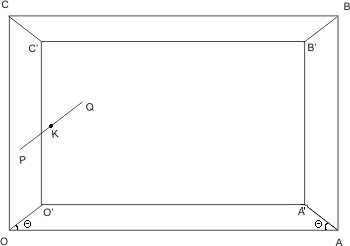
Ако центъра на отсечката PQ, т.е. т.K принадлежи на правоъгълника O'A'B'C', то и отсечката PQ ще лежи вътре в правоъгълник OABC. Ако намерим тази вероятност Pa, то ще знаем и вероятността на отсечката да пресече OABC - P = 1 - Pa.
|O'A'| = |OA| - |OO'|.cosΘ - |AA'|.cosΘ = a - l.cosΘ
|O'C'| = |OC| - |OO'|.sinΘ - |CC'|.sinΘ = b - l.sinΘ
Елементарната вероятност е PΘ = dΘ/π
=> 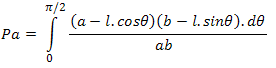 =>
=> ![]()
=>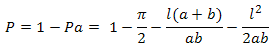
Добави коментар