C, PHP, VB, .NET

Задача: В равнината имаме мрежа от еднакви триъгълници с лице F и със страни a, b и c и ъгли α, β и γ. Каква е вероятността отсечка PQ с дължина l, по-малка или равна на най-късата височина на триъгълника, да лежи изцяло в някой триъгълник?

Решение: Нека вземем един от триъгълниците и го означим с ABC. Построяваме координатна система с ос Ox минаваща по отсечката AB. Нека ъгъла, който отсечката PQ сключва с оста Ox е θ.

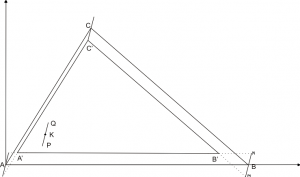
Прекарваме три отсечки с центрове върховете A, B и C, успоредни на PQ и с дължина l. От върховете двете от тези построени отсечки, които са изцяло извън триъгълника ABC, построяваме успоредни прави на страните на триъгълника и взимаме пресечните им точки (без да ограничаваме множеството на решенията ще ги приемем за A' и B', защото означенията на върховете на ABC могат да се променят). Нека върха на построената отсечка, чиято половина лежи вътре в триъгълник ABC я наречем C'. Получаваме триъгълник A'B'C':

Ако центърът на иглата PQ (точка K) лежи вътре в триъгълник A'B'C', то самата игла ще лежи изцяло вътре в триъгълник ABC.

Елементарната вероятност е:

Да изчислим дължината на отсечката A'B': |A'B'|= |AB| - |B'N'|.

От триъгълник MB'N се вижда, че:

Така и чрез  A'C' можем да изчислим вероятността на точка K да лежи вътре в триъгълника (спрямо точката A):

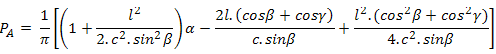
Заместваме циклично a, b и c и съответно α, β и γ и така получаваме P_B и P_C. Така окончателно получаваме P = P_A + P_B + P_C

=>

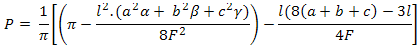
Задача: При всяко a, b и c (изпълняващи условията за съществуване на триъгълник) ли може да се построи плътна мрежа от триъгълници в равнината?

Задача: Как ще се реши задачата, ако l е поне по-голямо от най-малката височина на триъгълника?