C, PHP, VB, .NET

Задача: Избираме четири произволни точки от единичен кръг. Каква е вероятността те да са върхове на изпъкнал четириъгълник?

Решение: Нека точките са A₁, A₂, A₃ и A₄. Линиите A₁A₂, A₂A₃ и A₃A₁ разделят кръга на 7 части, например:

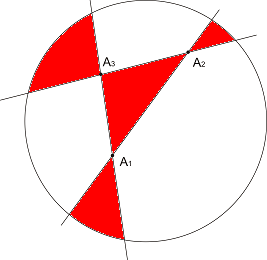
Ако четвъртата точка A₄ принадлежи на „белите“ части, то четириъгълника ще бъде изпъкнал. Ако точка A₄ принадлежи на „червените“ части, то четириъгълника ще бъде вдлъбнат.

Вероятността точка A₄ да принадлежи в „червената област“ на триъгълник A₁A₂A₃ е равна на лицето на триъгълника E разделено на лицето на окръжността (π). Колкото до останалите „червени области“ можем да кажем, че средната стойност на очакваните им лица E_i (спрямо връх A_i, i=1,2,3) е равна на средната стойност на очакваното лице на триъгълника Е. Това е така, защото можем да разгледаме тези области като ги вземем предвид за вероятността на т.A_i да лежи вътре в триъгълник A_jA_kA₄ (където i=1,2,3; j=2,3,1 и съответно k=3,1,2). Така E₁ = E₂ = E₃ = E.

От тук можем да заключим, че вероятността за A₁A₂A₃A₄ да бъде изпъкнал е равна на лицето на „белите области“ разделено на лицето на кръга:

P(A₁A₂A₃A₄) = (π – 4E)/π

Така задачата ще бъде решена когато изчислим средната стойност на очакваното лице на триъгълника S(A₁A₂A₃) = E. Решението на задачата дадено от университетът в Бингхамптън за тази задача (което впрочем и досега следвахме 1:1) показва, че E = 35/(48π)

=> P(A₁A₂A₃A₄) = 1 – 35/(12π²)

Обобщение за всякакъв кръг: Оказва се, че намерената вероятност е инвариантна спрямо радиуса на кръга. Действително ако решите същата задача за кръг с радиус r ще видите, че отново P(A₁A₂A₃A₄) = 1 – 35/(12π²)