* Обобщена задача на Силвестър за четирите точки
Публикувано на 30 март 2010 в раздел Вероятности.
Задача: Нека имаме четири произволни точки в изпъкнала област K. Намерете вероятността те да са върхове на изпъкнал четириъгълник.
Решение (без доказателство): Оказва се, че въпреки, че решенията са независими от големината на областта, все пак според вида на K се получават различни решения. Оригиналното решение на Силвестър от 1865г. е дадено в област триъгълник. Там вероятността се оказва 2/3. По късно Цзубер доказва, че вероятността P получава минимум именно в такава област K (триъгълник).
Крофтон през 1885г. е дал решение на задачата за области квадрат (вероятност P=25/36), правилен шестоъгълник (P=683/972) и кръг, което разгледахме вече в задача за четирите точки на Силвестър за кръг (P=1–35/12π2).
Така постепенно се стигнало до заключението, че минимума на вероятността се постига при област триъгълник, а максимума при област елипсоид. Грьомер е доказал, че максимума се достига именно при n-мерен елипсоид.
През 1994г. Е. Гецаиушкаш от института по математика и информатика във Вилнюз дава следната обобщена формула при изпъкнала област K (решение чрез т.нар. "метод на хордите"):
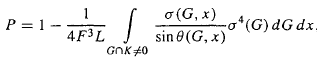
където L и F са периметър и лице на областта K; dG = dpdρ е гъстотата на линиите; p и ρ са нормалните координати на линия G; σ(G) е дължината на хорда G∩K; σ(G,x) е дължината на хорда перпендикулярна на линия G и минаваща през точка x на линията G; Θ(G,x) е ъгълът между тангентата и удължението на хордата с дължина σ(G,x) в точката пресичаща контура.
Добави коментар