C, PHP, VB, .NET

Днес се сблъсках с една много интересна и определено класическа задача за геометрични вероятности. Нека първо покажа оригиналното решение, а после и пример как компютърното моделиране не винаги води до правилни резултати:

Задача: Каква е вероятността един произволен триъгълник в равнината да бъде остроъгълен?

Решение: Нека ъглите на триъгълника са α,β и γ. Знаем, че α+β+γ = 180 (1) и освен това α>0, β>0 и γ>0 (2,3,4). Ако построим ортонормирана координатна система и по осите и нанасяме стойностите на α, β и γ, то условието (1) ще определи една равнина. Сечението на тази равнина с "първи квадрант" (определен от условията за полуравнините (2,3,4)) ще определи един триъгълник:

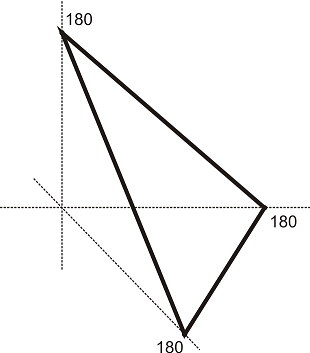
Този триъгълник (въпреки, че не си личи от чертежа поради гледната точка) е равностранен. Ако вземем произволна точка в този триъгълник, то тя еднозначно определя стойности за α, β и γ, които разгледани като ъгли на триъгълник удовлетворяват условието за съществуването му (α+β+γ=180).

Нека сега разгледаме кога този триъгълник ще бъде остроъгълен. Очевидно това е когато α<90, β<90 и γ<90. Това означава, че точката (произволният триъгълник) ще трябва да бъде заключена "зад" равнините α=90, β=90 и γ=90:

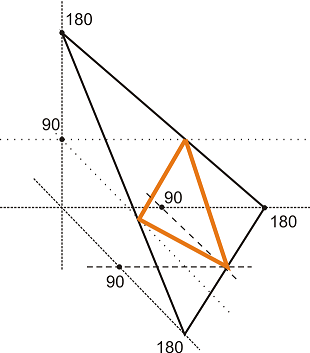
Именно ако произволна точка (триъгълник) попадне вътре в червения триъгълник, то ще имаме "добър изход", т.е. остроъгълен триъгълник. Нека разгледаме графиката в равнината на равностранния триъгълник, за да стане още по-ясно:

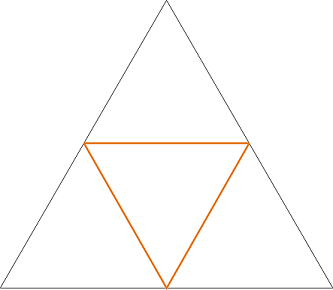
Е, от тук нататък задачата се свежда до решаването на задачата "каква е вероятността за произволна точка в равностранен триъгълник да попадне в триъгълника определен от центровете на страните".

=> P = S(червен триъгълник) / S(черен триъгълник)

=> вероятността произволен триъгълник да бъде остроъгълен е P = 1/4

Край на класическото решение.

Интересно е, че в интернет масово хората решават задачата използвайки компютър и получават доста по-различна вероятност - около 1/5, или за да бъда пределно точен - приблизително 0,19314715... Обикновено решенията се моделират като се вземат произволни координати на точките в равнината (общо 6 - по две координати за всяка точка) и според тях се прави проверка дали тръгълника е остроъгълен. При хиляди, дори стотици хиляди или милиони проверки, вероятността се получава именно клоняща към показаното число.

Разрових се и естествено открих къде се корени "проблема" - компютърните модели са ограничени и не могат за генерират безкрайно големи произволни числа. Генерираните произволни числа са лимитирани между 0 и L (горната граница на възможните за компютъра), т.е. точките са лимитирани в един квадрат със страни L, а не е в цялата равнина. Това дава съвсем различна задача и съответно различно решение, подобно на вариантите, които споменахме в обобщената задача на Силвестър.