C, PHP, VB, .NET

Нека решим още няколко задачи свързани с хиперсфери, като продължение на миналата тема за вероятност на „n“ точки в „полухиперсфера“. Ще разгледаме "обратната" (не случайно я наричам така) задача за намиране на вероятността центъра на окръжността да лежи вътре в многостена определен от точките. Вече решавахме една такава задача в двумерното пространство с окръжност и три точки, четири и n точки (виж задачи 1, 4 и 5 от положения на "n" точки в окръжност). Нека разгледаме следната задача за тримерното пространство:

Задача. Четири произволни точки лежат върху сфера с радиус 1 в тримерното пространство. Каква е вероятността центъра на сферата да лежи вътре в многостена определен от точките (взети като негови върхове)?

Решение: Знаем, че всеки две точки заедно с центъра на сферата определят равнина, която разделя сферата на две полусфери. Следователно всяка трета точка от сферата ще лежи или в едната или в другата полусфера, определена от предишните две точки, т.е. имаме условието "всеки три точки от сфера лежат в една нейна полусфера".

Нека вземем три от произволните точки и ги означим с A,B и C, а центъра на сферата е т.O. Те определят криволинеен триъгълник ABC върху сферата. Нека този триъгълник има лице "x". Построяваме лъчите AO, BO и CO, които пресичат сферата в точки A'. B' и C'. Ако четвъртата произволна точка D лежи в криволинейния триъгълник A'B'C', то центъра на окръжността ще бъде вътре в многостена ABCD и обратно - ако т.D е извън криволинейния триъгълник A'B'C', то т.O ще е извън многостена ABCD. Вероятността за това т.D да е вътре в многостена е (лицето на A'B'C')/(лицето на сферата), т.е. е равно на x/4π.

Лицето на криволинейния триъгълник ABC може да варира от 0 до 2π. Следователно вероятността т.О да е вътре в многостена ABCD е:

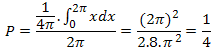
И при този метод няма изненада. Всъщност вероятността за това центъра на окръжността да лежи вътре в многостена е равна на вероятността четирите точки да НЕ лежат в една полусфера! Знаем от предишната статия, че вероятността четирите точки да лежат в една триизмерна полусфера е 3/4, следователно вероятността да НЕ лежат в една полусфера е 1-3/4=1/4.

Задача за упражнение 1. Проверете по описания по-горе метод дали вероятността за това многостен от пет точки да съдържа центъра на окръжността съвпада с вероятността петте точки да НЕ лежат на една равнина.

Задача за упражнение 2. Изведете обща формула за вероятността центъра на k-мерна хиперсфера да лежи вътре в многостен съставен от n на брой произволни точки лежащи върху хиперсферата, за n≥k+1.