C, PHP, VB, .NET

Задача: Дадена е окръжност "k" с радиус R=1. Върху тази окръжност са избрани три произволни точки, които взимаме за върхове на триъгълник. Каква е вероятността произволна точка от кръга "k" да попадне вътре в триъгълника?

Решение: Лицето на кръга е известно - π. Нужно е да се намери лицето на произволния триъгълник. Най-удобно в случая е да параметризираме триъгълника чрез неговите ъгли по следният начин:

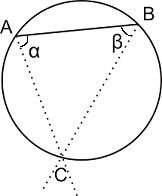Действително - знаейки ъглите α и β и радиуса на описаната окръжност, ние можем еднозначно да определим лицето на триъгълника по формулата (извежда се чрез синусова теорема):

S(α,β,R) = 2R².sin(α).sin(β).sin(α+β)

И понеже R=1 (по условие), то имаме:

S(α,β) = 2.sin(α).sin(β).sin(α+β)

и очевидно лицето на триъгълника зависи от ъглите α и β. Остава да преценим, че при положение, че точките са произволни, то ако ъгъл α може да се мени от 0 до π, то ъгъл β ще се мени от 0 до π-α. Получава се следния, лично за мен неприятен и труден, за решаване интеграл:

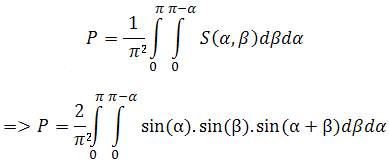
Програмата Mathematica 8 дава следния резултат:

In[1] = 2 Integrate[(Sin[x] Sin[y] Sin[x + y]), {x, 0, Pi}, {y, 0, Pi - x}]/Pi^2

Out[1]= 3/4π

=> (ако сметките на Mathematica са вярни)

P = 3/4π