* Произволен кръг спрямо координатна система
Публикувано на 24 декември 2010 в раздел Вероятности.
Задача: Имаме фиксирана координатна система Oxy в равнината. Каква е вероятността кръг с произволен център и произволен радиус да съдържа центъра на координатната система?
Решение: Нека първо разгледаме положението на центъра на координатната система и центъра на кръга. Радиус векторът е r:
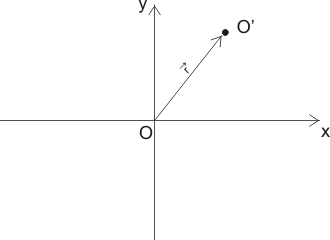Ако ние ротираме координатната система вероятността няма да се промени. Затова за удобство ще завъртим Oxy така, че остта „x“ да съвпадне по посока с радиус-вектора r:
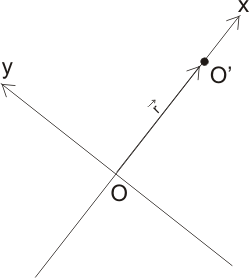
Нека сега върху остта x изберем втора произволна точка A, която в нашия случай ще се яви „пресечната точка на окръжността с правата Ox“. Тоест тази втора произволна точка ще определя радиуса на окръжността. Е, кръгът ще съдържа т.O тогава, когато |O’A|=R>|r|.
Следователно задачата се свежда до намирането на по-голямото от две произволни числа. Ние вече решавахме тази задача (виж обобщената задача при неограничено множество). Отговорът:
P=1/2
Добави коментар