* Квадрат и окръжност
Публикувано на 14 юни 2011 в раздел Вероятности.
Задача 1: В равнината е даден квадрат със страна 1. Вътре в квадрата избираме произволна точка, която се явява център на окръжност с радиус 1. Каква е вероятността квадратът да лежи изцяло вътре в окръжността?
Упътване: Квадратът ще бъде вътре в окръжността ако центъра на окръжността (произволната точка) лежи в защрихования в черно регион на следната картинка:
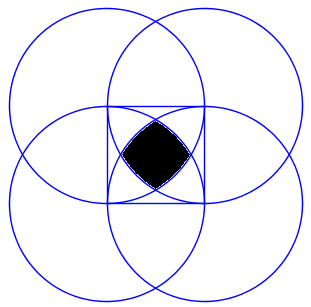Намерете лицето на региона (S(R)) и го разделете на лицето на квадрата (1). Това ще бъде търсената вероятност.
Задача 2. В пространството имаме даден куб със страна 1. Вътре в куба избираме произволна точка, която се явява център на сфера с радиус 1. Каква е вероятността куба да е вписан изцяло вътре в сферата?
Задача 3. Даден е n-мерен хиперкуб със страна 1. Вътре в куба избираме произволна точка, която се явява център на n-мерна хиперсфера с радиус 1. Каква е вероятността хиперкуба да е вписан изцяло вътре в хиперсферата?
Упътване: Първо се опитайте да решите задачата при n=4 и от там ще стане доста по-лесно...
Региона в черно може да се раздели на 4 равни части (чрез диагоналите му). Една такава част е представена в жълто на схемата:
Тя, заедно с 2та сиви триъгълника представлява сегмент от оркъжността, и този сегмент е 1/12 от лицето на окръжността. За да намерим лицето на жълтата част е достатъчно да намерим лицето на сивите триъгълници и да ги извадим от лицето на сегмента.
Няма да влизам в подробности защо 2те червени отсечки сключват ъгъл от 60 градуса - мисля че е ясно. Така ъгъла отбелязан с зелено остава да е 15 градуса. Имаме и 2 от страните на този тъмно сив тригъгълник - червената е единица, а тази която е част от диагонала на квадрата е sqrt(2)/2. Можем да определим лицето на сивите триъгълници, а от там и лицето на жълтата фигура. Остава да го умножим по 4 за да установим лицето на фигурата в черно обозначена в задачата. От там се намира и търсената вероятност.
Браво Бобев! Вярно решена задача 1! Леко ти редактирах коментара.
Лицето на триъгълника е: S(T)= √2(√6-√2)/16
Тогава лицето на двата триъгълника ще е √2(√6-√2)/8
Лицето на СЕКТОРЪТ (единствената забележка към това, което написа - не е сегмент, а е сектор) е Pi/12
=> лицето на жълтата част (Pi/12 - √2(√6-√2)/8)
Умножено по 4 дава вероятност около:
P = 0,31514674391769295770405152112117
За задача 3. Диагоналът на квадрат със страна 1 е √2, на куб със страна 1 е √3, на четиримерен куб със страна 1 е √4 и т.н. - n-мерен куб със страна 1 ще е √n.
Да се фокусираме върху 4-мерен хиперкуб със страна 1. Диагоналът му е √4=2. Единственият начин да се впише вътре във 4-мерно хиперкълбо с радиус 1 е центърът на кълбото да е точно в центъра на диагонала. Следователно вероятността е 0.
При по-големите размерности диагоналът на куба расте, а радиусът на кълбото не. Следователно при размерности за всяко n>3 вероятността е 0.
Остава да се реши задача 2. При нея трябва да се намери обема на фигурата, която се получава от пресичането на осем единични кълба, чийто центрове са върховете на куб със страна 1.
Финално ако се намери обща формула (въпреки, че леко безсмислено с оглед нулевите вероятности при размерност по-голяма от 3) темата ще бъде изчерпана.