C, PHP, VB, .NET

Задача. Дадено е квадратно уравнение [mathi]ax^2+bx+c=0[/mathi], където [mathi]a,b,c\in [-n,n][/mathi] са произволни реални числа. Каква е вероятността корените на квадратното уравнение да са реални числа?

Решение: Нека разгледаме два случая спрямо стойностите на "a":

I случай) а>0

Можем да разделим двете страни на равенството на "a", понеже то е различно от 0. Ще получим квадратното уравнение [mathi]x^2+\frac{b}{a}x+\frac{c}{a}=0[/mathi].

Полагаме [mathi]p=\frac{b}{a}[/mathi] и [mathi]q=\frac{c}{a}[/mathi]. Понеже [mathi]b,c\in [-n,n][/mathi], то от това полагане следва, че [mathi]p,q\in [-\frac{n}{a},\frac{n}{a}][/mathi].

От тук нататък решението се свежда до това, което беше дадено в предишната статия, но спрямо новия интервал. Ако положим [mathi]m=\frac{n}{a}[/mathi], то решението на задачата е:

1) [mathi]m=\frac{n}{a}\leq 4[/mathi], т.е. [mathi]a\geq \frac{n}{4}[/mathi]

[math]P_{a\geq \frac{n}{4}}^I=\frac{m+12}{24}=\frac{n+12a}{24a}[/math]

2) [mathi]m=\frac{n}{a} > 4[/mathi], т.е. [mathi]a < \frac{n}{4}[/mathi]

[math]P_{a < \frac{n}{4}}^I=1-\frac{2}{3\sqrt{m}}=1-\frac{2}{3\sqrt{\frac{n}{a}}}[/math]

II случай) а<0

Когато "a" е отрицателно число, отново ще разделим равенството на него: ще получим квадратното уравнение [mathi]x^2+\frac{b}{a}x+\frac{a}{c}=0[/mathi].

В този случай обаче в полагането трябва да отчетем, че коефициента пред x и сводобния коефициент са променили знака си. Защо това е проблем? Нека си припомним, че дискриминантата на квадратното уравнение в нашия случай ще е [mathi]D=(\frac{b}{a})^2-4\frac{c}{a}[/mathi]. Забележете, че [mathi]\frac{c}{a}[/mathi] си е сменило знака, но [mathi]\frac{b}{a}[/mathi] се повдига на квадрат и този минус се "губи".

Затова в този случай е нужно да положим [mathi]p=-\frac{b}{a}[/mathi] и [mathi]q=-\frac{c}{a}[/mathi]. Както в предишния случай понеже [mathi]b,c\in [-n,n][/mathi], то от това полагане следва, че [mathi]p,q\in [\frac{n}{a},-\frac{n}{a}][/mathi].

Тук вече получихме ново квадратно уравнение:

[math]x^2-px-q=0[/math]

Което трябва разбира се да решим. Ако положим [mathi]m=-\frac{n}{a}[/mathi], то в интервала [-10, 10] благоприятните изходи ще са защрихованата част от следната графика:

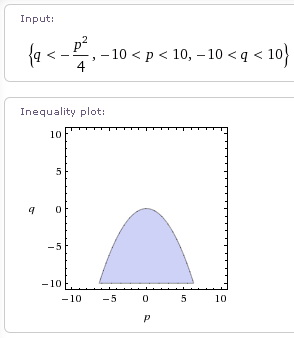Но това е точно обратната вероятност на тази от предишната точка (графиката и защрихованата област са огледални)! Следователно решението ще е:

[math]P_{-a\leq \frac{n}{4}}^{II}=1-\frac{n+12a}{24a}[/math]

[math]P_{-a > \frac{n}{4}}^{II}=1-1+\frac{2}{3\sqrt{\frac{n}{a}}}=\frac{2}{3\sqrt{\frac{n}{a}}}[/math]

Алтернативно наблюдение: Можехме да подходим към решаването на задачата, чрез изчисляване на [mathi]b^2-4ac>0[/mathi]. Тогава трябваше да изчисляваме обеми (двойни интеграли). Графиката е следната:

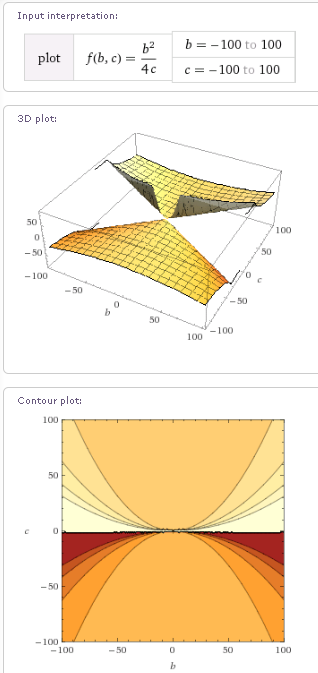
И на тази графика се вижда, че графиката от положителната страна на "a" (a=f(b,c)) е огледална на тази от отрицателната страна на "a". Тоест и вероятността е обратна.

Обобщен отговор: Крайният отговор се получава като обединим двата случая:

[math]\begin{array}{l}P(|a|\geq \frac{n}{4})=P(a>0).P(a\geq \frac{n}{4})^I + P(a<0).P(-a\leq \frac{n}{4})^{II}=\\=\frac{1}{2}.\frac{n+12a}{24a}+\frac{1}{2}.(1-\frac{n+12a}{24a})=\frac{1}{2}\end{array}[/math]

[math]\begin{array}{l}P(|a|\leq \frac{n}{4})=P(a>0).P(a < \frac{n}{4})^+P(a<0).P(-a > \frac{n}{4})^{II}=\\=\frac{1}{2}\left(1-\frac{2}{3\sqrt{\frac{n}{a}}}+\frac{2}{3\sqrt{\frac{n}{a}}}\right)=\frac{1}{2}\end{array}[/math]

Или виждаме, че за всяко [mathi]n[/mathi] имаме една и съща вероятност. Следователно вероятността едно квадратно уравнение [mathi]ax^2+bx+c=0[/mathi] с произволни [mathi]a,b,c\in [-n,n][/mathi] да има реални корени е:

[math]P=\frac{1}{2}[/math]

П.П. Не претендирам за верни отговори и сметки. Възможно е да има грешки.