C, PHP, VB, .NET

Вземете една окръжност и изберете N на брой точки върху нея така, че разстоянието между две съседни точки да е винаги едно и също. Изберете три произволни точки. Каква е вероятността да формирате правоъгълен триъгълник с тях?

При N=8 чертежът е следния:

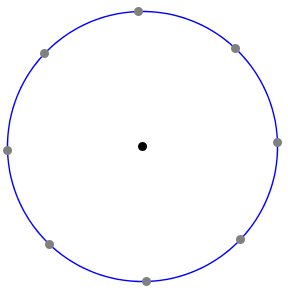
Ясно е, че за да бъде правоъгълен триъгълника, две от точките трябва да лежат на диагонал на окръжността (центъра на описаната около правоъгълен триъгълник окръжност лежи върху неговата хипотенуза). Нека подходим по индукция.

При N=3 имаме три точки и можем да изберем само тях. Те обаче образуват равностранен, а не правоъгълен триъгълник. Следователно вероятността е 0.

При N=4 имаме вписан в окръжността квадрат. Които и три точки да изберем, винаги две от тях ще са срещуположни върхове на този квадрат, т.е. лежат на диагонал на окръжността. Следователно тук вероятността е 1.

При N=5 отново вероятността ще е 0, защото няма две точки, които да са срещуположни. В този случай вероятността ще е 0.

Изобщо още от тук можем да обобщим, че за всяко нечетно N вероятността е 0. Ако две точки лежат на диагонала, то те разделят окръжността на две половини и във всяка половина трябва да има по равен брой точки. Така ако вземем точките да са N=2K+1 (нечетно число) и от тях извадим 2-те точки, които предполагаме, че лежат по диагонала, то ще останат 2K-1 налични точки – нечетно число. Целите нечетни числа не се делят на две, значи не може да има по равен брой точки в двете половини на окръжността. От тук следва, че предположението е грешно и не е възможно при нечетен брой точки две от тях да лежат на диагонал. От тук и вероятността да изберем три и те да формират правоъгълен триъгълник е 0.

Нека продължим с индукционните наблюдения. При N=6 трябва да изберем три точки от шест възможни. Комбинациите без повторения се намират по формулата:

[math]S = \frac{6!}{3!.(6-3)!}=\frac{6.5.4}{3.2.1}=20[/math]

Има общо три възможни диаметъра, за всеки от които могат да се формират общо по четири правоъгълни триъгълника. Значи има общо 12 правоъгълни триъгълника. Така намираме вероятността:

[math]P(N=6) = \frac{12}{S}=\frac{12}{20}=\frac{3}{5}[/math]

Класическата задача е при N=8.Общият брой възможни триъгълници се получава лесно по формулата за комбинация на три елемента от осем без повторения:

[math]S = \frac{8!}{3!.(8-3)!}=56[/math]

Имаме общо 4 възможни диагонала, с всеки от които може да се направят по 6 правоъгълни триъгълника, т.е. общо 24. Следователно вероятността е:

[math]P(N=6) = \frac{24}{S}=\frac{24}{56}=\frac{3}{7}[/math]

Време е да обобщим за N=2K (четно число). Общият брой триъгълници ще бъде:

[math]S = \frac{2K!}{3!.(2K-3)!}=\frac{2K.(2K-1).(2K-2)(2K-3)!}{3!.(2K-3)!}=\frac{K.(2K-1)(2K-2)}{3}[/math]

Що се отнася до правоъгълните триъгълници, за тях имаме общо N/2 = K на брой диагонала, а с всеки диагонал ще могат да се направят N-2 = 2K-2 триъгълника, т.е. общо K.(2K-2) правоъгълни триъгълника. Така намираме вероятността:

[math]P(N=2K) = \frac{K.(2K-2)}{S} = \frac{3.K.(2K-2)}{K.(2K-1)(2K-2)}=\frac{3}{2K-1}[/math]

Обобщено отговорът на задачата е:

[math]\left|\begin{array}{l}P(N odd)=0\\P(N even)=\frac{3}{N-1}\end{array}\right.[/math]