C, PHP, VB, .NET

Да припомним задачата: Дадена е окръжност с радиус R. Изберете две произволни точки лежащи върху окръжността. Какво е очакваното разстояние (по права линия) между точките?

В предишната статия показах метод, чрез който се получаваше решение [mathi]D =\frac{4R}{3}[/mathi]. Сега ще покажа друг метод, чрез който се получава друг, леко различен отговор.

Правата през първата точка и центъра на окръжността разделят окръжността на две огледални части. Втората произволна точка ще попадне или в едната или в другата част.

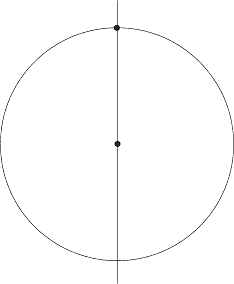
Нека предположим, че втората точка е попаднала в лявата част. Правата, която минава през центъра на окръжността и е перпендикулярна на правата, която вече построихме, ще пресече окръжността точно в центъра на лявата дъга:

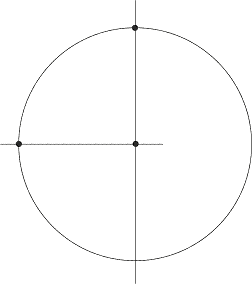
Понеже е точно в центъра, то от всички възможни произволни точки лежащи на тази дъга, тази ще бъде „средната“, т.е. очакваната. Сега вече е лесно да намерим очакваното разстояние по Питагоровата теорема:

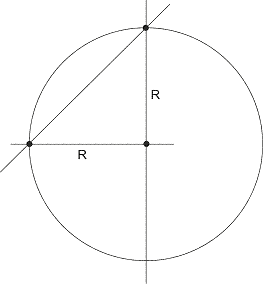
Така намираме, че очакваното разстояние, ако втората точка е попаднала в лявата половина, е [mathi]D = \sqrt{2}R[/mathi]. Да, но положението от дясно ще е абсолютно същото (имаме пълна симетрия). Следователно решението на задачата е:

[math]D = \sqrt{2}R[/math]

Как стои въпроса с триизмерното пространство, т.е. ако точките се намират върху сфера? И с този метод няма да има разлика. Ако изберем едната точка да бъде образно казано „северния полюс“, то средното положение на втората ще бъде да лежи някъде по „Екватора“ (който в нашия случай е окръжност). А разстоянието от първата точка (Северен полюс) до която и да е точка от този „Екватор“ е едно и също – [mathi]D = \sqrt{2}R[/mathi]. Предполагам, че „нагоре“ в по-големи размерности положението е същото.

Но нека не свършваме толкова бързо. Нека разгледаме друга възможна параметризация – с полярни координати. Нека изберем първата точка да се намира в координати [mathi](R, 0)[/mathi] – т.е. ъгъла е 0 градуса, а центъра на окръжността е в началото на координатната система. Тогава координатите на втората точка ще се различават от първата точка по ъгъла, т.е. тя ще е с координати [mathi](R, \varphi)[/mathi]. Тогава разстоянието между точките ще бъде:

[math]d=\sqrt{R^2 + R^2 – 2RR. cos(\varphi)} = R\sqrt{2-2.cos(\varphi)}[/math]

Разглеждаме само „горната половина“ на окръжността (долната е симетрична). Ъгълът ще се мени в интервала [mathi][0,\pi][/mathi]. Следователно имаме средно разстояние:

[math]D = \frac{\int_0^{\pi} {R\sqrt{2-2.cos(\varphi)}}}{\pi} = \frac{4R}{\pi}[/math]

Откъде идва разликата между предложеното в предишната статия решение и двете предложени в тази? В решението от предишната задача получихме решение приблизително равно на 1,333R, в първия метод от тази статия получихме решение, което е приблизително 1,414R, а в третия метод получихме решение приблизително 1,273R? Отговорът е подобен на казуса в задачата на Бертран – имаме различна гъстота на решенията. Начинът на моделиране на решението предопределя вероятността! Реално последната (полярната) параметризация ще дава най-добро разпределение на решенията, съответно именно тя би трябвало да бъде определена като най-правилна. В сайта на Майкъл Якобсен има симулация, която потвърждава това мнение.